Proving Cantor’s theorem in Lean 4

Tuesday July 23 2024

In this post I walk through proving Cantor’s theorem in Lean 4. Along the way we will encounter some fundamental ideas in dependent type theory, as well as the Lean language.

The intended audience are people new to automated theorem proving. Parts 1-2 will review Cantor’s theorem. Skip to Part 3 if you know the theorem to jump straight into Lean.

If you want to tinker with the code without installing Lean, check out live.lean-lang.org

1. Informal statement of Cantor’s theorem

To begin, recall Cantor’s theorem:

Cantor’s theorem: Let \(S\) be a set, and let \(P(S)\) be the power set of \(S\). Then there is no surjective function from \(S\) to \(P(S)\).

If these words are unfamiliar, no worry, let’s define them:

• a set is a collection of elements. We can list the elements of a set using brackets like \(S = \{...\}\). We write \(x \in S\) to mean that \(x\) is an element of \(S\) and \(x \notin S\) otherwise. Sets can be finite or infinite.

• the power set is the collection of all subsets. For example if \(S = \{1,2,3\}\) then \(P(S) = \{\{\}, \{1\}, \{2\}, \{3\}, \{1,2\}, \{1,3\}, \{2,3\}, \{1,3,3\}\}\). Notice how we included the empty set \(\{\}\).

• a function between sets assigns elements of one set to another, i.e. if \(A\) and \(B\) are sets then \(f:A \to B\) denotes a function from \(A\) to \(B\), so that each element \(a\) in \(A\) is assigned to an element \(f(a)\) in \(B\). \(A\) is called the domain and \(B\) is called the range (or codomain). Functions can only assign each element of the domain to one element of the range. Multiple elements of the domain can be assigned to the same element in the range, and not every element in the range need be assigned to.

• a function is surjective if every element of the range is assigned to by some element of the domain. For example if \(A=\{1,2,3\}\) and \(B=\{4,5,6,7\}\) and \(f:A\to B\) is the function defined by \(f(1)=4\), \(f(2)=5\), and \(f(3)=6\), then \(f\) is not surjective because no element is assigned to \(7\). In other words, there does not exist an \(x\) in \(A\) such that \(f(x)=7\). More generally, a function \(f: A \to B\) is surjective if for all \(b \in B\), there exists \(a \in A\) such that \(f(a)=b\).

If \(B\) has more elements than \(A\), then it is impossible for there to be a surjective function \(A \to B\). In fact, this proves Cantor’s theorem whenever \(S\) is finite, because if \(S\) has \(n\) elements, then \(P(S)\) has \(2^n\) elements, and \(n\) is less than \(2^n\). But Cantor’s theorem holds more generally in the case when \(S\) may be be infinite.

2. Informal proof of Cantor’s theorem

To prove Cantor’s theorem, let \(S\) be a set, let \(P(S)\) be its power set, and let \(f: S \to P(S)\) be any function. We will show \(f\) cannot be surjective using a proof by contradiction. To do so, assume \(f\) is surjective with the goal of deriving a contradiction.

Because \(f\) is surjective, every subset must be assigned to by some element of \(S\). Consider the following subset:

\[ B = \{ x \in S \mid x \notin f(x) \} \]

Since we assumed \(f\) is surjective, there must exist some \(x^*\) in \(S\) such that \(f(x^*) = B\). But this yields a contradiction. Observe:

• if \(x^* \in B\), then \(x^* \notin f(x^*)\), and \(f(x^*)=B\), so \(x^* \notin B\), a contradiction.

• if \(x^* \notin B\), then \(x^* \in f(x^*)\), and \(f(x^*)=B\), so \(x^* \in B\), a contradiction.

Both cases result in contradiction, so this negates the original assumption that \(f\) is surjective and completes the proof by contradiction.

3. Formal statement of Cantor’s theorem

Lean is based on dependent type theory where we work (roughly speaking) with types instead of sets. If T is a type, then x : T means x is a term of type T, analogous to x belonging to T as a set.

def surjective {A B : Type} (f: A → B) : Prop :=
  ∀ b : B, ∃ a : A, f a = b

Some remarks:

• Lean definitions takes the form x : T := expr where x is the name of the term, T is its type, and expr is an expression providing the definition.
• This code block defines a new term called surjective. The type of this term is a dependent function type, whose inputs are the types A and B along with a function f: A → B and whose output is the proposition that f is surjective.
• {A B : Type} is wrapped in brackets while (f: A → B) is wrapped in parentheses, they are functionally similar but somewhat of a stylistic choice, it says that the types A and B can be implicitly inferred from f, and the result takes a single input f and returns a true or false proposition.
• ∀ means “for alL” and ∃ means “there exists”, the definition matches the one given earlier in section 1.
• f a = b is notation for f(a) = b

Exercise: state (but don’t prove) the theorem that the composition of two surjective functions is surjective.

def composition_of_surjective_is_surjective (A B C: Type) (f: A → B) (g: B → C) (h1: surjective f) (h2: surjective g) : surjective (g ∘ f) :=
  sorry

def subset (A: Type) : Type := A → Prop

Can you figure out what is going on? This definition takes a type A as input, and yields a new type, the type of functions from A to Prop (propositions). That’s what a subset is! It is a function that says yes/no on each element, determining whether it belongs to the subset. Thus, subset A is the type of all such functions, that is, the collection of all subsets.

theorem Cantor (A: Type) (f: A → subset A) : ¬ surjective f :=
  sorry

¬ is the symbol for negation. The theorem says for any type A, for any function f mapping terms of type A to terms of type subset A, then f is not surjective.

4. Formal proof of Cantor’s theorem

Proofs in Lean take place by a series of tactics. These tactics transform the goal state in sequence until the proof is completed. Normally the intermediate goal states are not visible when reading Lean source code, but I will display them to give a sense how the proof works.

theorem Cantor (A : Type) (f : A → subset A) : ¬ surjective f := by
  -- Begin proof by contradiction
  apply Not.intro
  -- Introduce contradictory hypothesis (that f is surjective) as h0
  intro h0
  -- Define the "bad" subset B
  let B : subset A := fun x => ¬ (f x) x
  -- Show that x is an element of B if and only if x is not an element of f(x)
  have h1 : ∀ x: A, B x ↔ ¬ (f x) x := by
    intros
    rfl
  -- Since f is surjective, let z be the element of A such that f(z) = B
  obtain ⟨z, h2⟩ := h0 B
  -- From h1, it follows that z is an element of B if and only if z is not an element of f(z)
  have h3 : B z ↔ ¬ (f z) z := h1 z
  -- But f(z) = B, so this is a contradiction. Hard to explain this part, it just works
  rw [h2] at h3
  have h4 : B z → False := fun x => h3.1 x x
  exact h4 (h3.2 h4)

TODO

Refuse to forfeit impractical thinking

Thursday July 11 2024

I may have failed to complete graduate school, but I refuse to forfeit impractical and abstract thought and be made to think about trivial practical things.

Two things you can’t get back

Thursday July 4 2024

are people and time.

Autoprosecution

Thursday July 4 2024

AI lawyers sound cool for interpreting legal text until they’re deployed en masse as federal prosecutors under a GOP regime.

Goals vs behavior

Wednesday July 3 2024

An “agent” is a system that takes actions in order to achieve a goal, and “intelligence” measures its competence at doing so.

But how does an agent know it has achieved its goal? The goal being achieved is a property of the state of the world, something for which the agent only partially observes.

In reinforcement learning, you can address this using the very sparse reward, +1 for being in the goal state and 0 otherwise. This should encourage the agent to learn a representation of the world it can use to distinguish a goal state from a non-goal state.

But something seems amiss. The agent’s true goal is to receive +1 reward, not for the world to be in the goal state. I guess this is the alignment problem.

Is there a way to make an agent genuinely interested in the true state of the world?

This paper seems relevant: Ontological crises in artificial agents’ value systems by Peter de Blanc (2018). He seems to describe the same problem:

One way to sidestep the problem of ontological crises is to define the agent’s utility function entirely in terms of its percepts, as the set of possible percept-sequences is one aspect of the agent’s ontology that does not change. Marcus Hutter’s universal agent AIXI [1] uses this approach, and always tries to maximize the values in its reward channel. Humans and other animals partially rely on a similar sort of reinforcement learning, but not entirely so.

We find the reinforcement learning approach unsatisfactory. As builders of artificial agents, we care about the changes to the environment that the agent will effect; any reward signal that the agent processes is only a proxy for these external changes. We would like to encode this information directly into the agent’s utility function, rather than in an external system that the agent may seek to manipulate.

Also The lens that sees its flaws by Yudowsky

Project 2025 scary

Tuesday July 2 2024

Scotus just gave presidential immunity. There is a lot of fear of losing democracy going around… AOC has called for some of the justices to be impeached. It seems comparable to the Enabling act of 1933.

It is very frightening for the election to be only a few months away. I don’t have anything to input, just recording my feelings.

What makes full?

Monday July 1 2024

What makes full human life? To have magnamity, shape your surroundings and face the consequences of your actions? Or to be part of a collective? Some people want to put trillions of humans in space but that thought disturbs me.

Existential disturbance

Monday July 1 2024

Sometimes reading people from past makes me feel one and at peace with the whole of humanity. Other times it makes me feel like a helpless worm…

Assume you will survive

Friday June 28 2024

If you are faced with two possible scenarios, one in which you survive and one in which you don’t, you should behave as if you are in the one in which you do.

This is a variation of Pascal’s wager. I can’t think of any good examples.

The mathematical auto-coder🤖⌨️☑️

Sunday June 23 2024

I am dreaming of a system that generates provably-correct code given user specifications. That is, the system takes a specification as input and yields two outputs, a piece of code, and a proof that the code meets specification. In other words, two generation steps, code generation and proof generation.

Some important people:

• Talia Ringer

Book compressing

Thursday June 20 2024

Call me stupid, but when I am reading some old book like Notes from the Underground I find like 25-50% of the text to be unnecessary and compressible. I want an LLM algorithm to compresses old books like this into more accessible less verbose versions. Maybe that would revive and reduce the culture barrier to old ideas. One problem is mistakenly removing important quotes and esoteric references.

Edit: someone already made this and called it “magibook” lol

Nocturnal panic feels

Wednesday June 19 2024

like being stranded in a tiny dinghy in a stormy sea on a black night.

Are corporations not already superintelligent AI?

Tuesday June 18 2024

I don’t really like the term “AI”, partly because it’s been overloaded by generative models like GPTs, but also what even is “artificial” - a non-descendant of LUCA?

I prefer the term intelligent agent or simply “agent”. An agent is an entity that takes actions to achieve goals. Biological life forms appear to be agents, with humans the most intelligent. According to instrumental convergence, agents tend towards self-preservation, resource acquisition, and self-improvement. Therefore, the existence of an agent with superhuman intelligence (aka superintelligence) would pose an existential risk to humanity.

Sounds right- but wait, aren’t companies, corporations, and nations already like this? Why do these entities not already pose existential risk, or do they? Is it because they are composed of human workers/managers/executives and thus depend on their existence? Are they simply not intelligent enough? Or are they not even “agents”?

People have discussed this:

1. Corporations vs. superintelligences by Eliezer Yudowsky (2016).

2. Things that are not superintelligences by Scott Alexander

3. Video essay: Why Not Just: Think of AGI Like a Corporation? by Robert Miles (2018) (click here for transcript).

4. Reviewing the Literature Relating Artificial Intelligence, Corporations, and Entity Alignment by Peter Scheyer (2018).

5. How Rogue AIs may Arise by Yoshua Bengio (2023)

6. Multinational corporations as optimizers: a case for reaching across the aisle on LessWrong (2023)

7. AGI alignment should solve corporate alignment on LessWrong (2020)

8. Organisations as an old form of artificial general intelligence by Roland Pihlakas (2018).

9. AI Has Already Taken Over. It’s Called the Corporation by Jeremy Lent (2017).

Most of the sources listed agree that corporations are intelligent agents, and furthermore they possess general intelligence by merit of being made of humans who have general intelligence. They tend not to believe, however, that corporations are superintellignt.

The problem seems to be their inability to combine the intelligence of their members. The main ways to do this are

• aggregation, where a large number of individuals work on the same task. For example, a board room has everyone come up with an idea, and they select the best idea.
• specialization, where each individual becomes best at a single task. For example, an engineering team consisting of mechanical, computer, and software engineers.
• heirarchy, where teams of individuals work (via above methods) on some task and send the result to their superior. For example, a military chain of command.

Notice all these methods are bottlenecked by human intelligence in some way. Aggregation is limited by the smartest human in the room, and specialization is limited by the smartest human at each task.

Heirarchy is an interesting case, because individuals at higher levels deal with more abstract concepts and are thus enabled to do higher-level reasoning. This is similar in neural networks where later layers deal with higher-level features.

Soldiers deal with the mechanical details of their weapons and vehicles, commanders think in terms of squadrons and battlefield positions, and generals thing in terms of grand strategy. But still, the general is a human and so the grand strategy will be explainable in human terms, something not to be expected of a superintelligent AI.

Robert Miles made this point well:

Corporations are able to combine human intelligences to achieve superhuman throughput, so they can complete large complex tasks faster than individual humans could. But the thing is, a system can’t have lower latency than its slowest component. And corporations are made of humans, so corporations aren’t able to achieve superhuman latency. […] Corporations can get a lot of cognitive work done in a given time, but they’re slow to react. And that’s a big part of what makes corporations relatively controllable: they tend to react so slowly that even governments are sometimes able to move fast enough to deal with them. Software superintelligence, on the other hand, could have superhuman throughput and superhuman latency, which is something we’ve never experienced before in a general intelligence.

Important footage

Thursday June 13 2024

Today I found some colorized footage depicting aftermath of the two main horrors of the second world war (I will link them below). Not light watching, but very emotionally moving. Colorization despite being artificial and often subtely wrong makes the footage much more visceral.

After watching it I felt a weird contrast between what I just watched, arguably some of the most important documented footage in history, and some recent AI generated video tech such as Sora, Kling, Luma, etc. Such a contrast that I felt disgusted with a lot of “generative AI” in general.

Why do we archive data at all? I guess two reasons, to record history and for entertainment. The latter, novels/songs/movies etc. is perhaps also a form of recording by the way of synthesizing and aggregating a lot of various lived experienced, even if the particular thing is fictitious. But generative AI slop doesn’t seem to be recording much of anything. If anything it makes all the real important footage like the aforementioned less trustworthy, which is a terrible outcome. So are the engineers working on generative AI a bunch of useful idiots serving totalitarian dictators or do they think they are doing something good by democratizing freedom of expression?

Video references (warning: graphic)

• “Hiroshima-Nagasaki, August 1945” produced by Erik Barnouw in 1970, original footage recorded by Akira Iwasaki in 1945.
  • colorized: https://www.youtube.com/watch?v=m4zZRy0GDcE
  • original: https://archive.org/details/hiroshimanagasakiaugust1945
• “Belsen Concentration Camp”, recorded in 1945 and used as evidence in the Nuremberg trials.
  • colorized: https://www.youtube.com/watch?v=mgwWq2cp2qM
  • original: https://catalog.archives.gov/id/24025

Being stupid

Wednesday June 12 2024

I find myself pretty stupid.. I am not good at slow deliberate thinking. I’m also not very good at reading, even though there are a lot of books, I am tantalized by their existence. So I’m left to think thoughts people already had and about dumb things like jobs and money.

Existential panic

Wednesday June 12 2024

This post may sound pretentious but it’s about something I find genuinely emotionally distressing. I am currently dealing with panic disorder, which is a very terrible thing, and often the panic comes at certain times of day without any particular reason. It tends to pull my mind towards thoughts of peril and doom and decay, essentially death. These concepts I can handle: we all die, it is a fact of life, and that is fine with me by now; besides I am young and relatively healthy and death is far away.

But there is another type of thought I absolutely cannot reconcile, which I guess is the feeling of existential absurdity. Why am I here? in this form, in this body, on this planet, in this universe? I am a biological life form, generated by evolution - not just that but a human being? And I’m me while I watch fellow humans blow each other apart in war, fellow people I could have just as easily been in (and in some sense maybe am in a parallel life). Why is any of this real? Am I like, god experiencing my own creation? Or I am trapped in hell? What the fuck is any of this?

For those thoughts I don’t have a quick calming answer for myself.

Future thinking

Wednesday May 29 2024

Don’t feel very good about future of humans today. I saw polls about increasing bigotry among youths in Netherlands. It is probably due to social media algorithms. So while the youth becoming increasingly fascist, the planet is warming and basic living conditions deteriorating. It gives me sick feeling in my stomach because I don’t see how humanity can recover except for a long periods of war and struggle that I won’t live to see the end of. It also feels like normal methods of human government like organizations and committees don’t work anymore against global powers and internet algorithms. What nightmare being created.

Idea and being

Tuesday May 28 2024

Was reading about demographics problems in Korea, not enough people having children so they pay you to get reverse vasectomy and trying to start government-run Tinder. Like in America, these stupid ideas are a bandaid fix for real problems: unaffordable housing, childcare, and other shitty living conditions. Then I also read about the feminist 4B movement which says: no sex, no children, no dating, no marriage. Badass!

Anyway, at home, some people close to me going through breakup despite having two childs. Sad for them. They already considered it before, but put it off and had child 2, then finally broke up anyway. I wonder if they made a few different decisions, if child 2 would never exist?

It makes me think, before we are born, we are just an idea in our parents’ (or parent’s) mind. The idea becomes reality and we exist. So there seems to be some equivalence between those two. Humans exert a lot of power over the world, the future is very much deteremined by the ideas in peoples’ minds, which gradually transform into material being.

Bonus reading: the non-identity problem aka the “paradox of future individuals”. Here’s an example: Suppose some company wants to build a dirty polluting factory in some uninhabited region which is sure to attract young workers and families and business, and thus future generations of inhabitants. But some environmentalist complains that those future generations, the children of the workers, will be at risk of cancer due to the polluting factory, so it would be wrong to build it. But without the factory, those children wouldn’t have been born, so how can it be wrong when the alternative is for them to not even exist?

One in a million chance

Tuesday May 14 2024

I’ve been wasting time on Turtle WoW lately and reminded of a classic problem in probability.

If a rare event has a 1-in-100 chance to occur, and you repeat it 100 times, it is guaranteed to happen right?

Not quite. The negative binomial distribution for it gives us the following formula for the chance of success after 100 attempts:

\[ 1 - \left( 1 - \frac{1}{100}\right)^{100} \,=\, 0.6339... \]

In fact, replace a 1-in-100 chance with 1-in-million chance, and the result will be about the same after a million attempts:

\[ 1 - \left( 1 - \frac{1}{1000000}\right)^{1000000} \,=\, 0.6321... \]

What is this magical 63% number? It turns out to be a constant related to Euler’s number given by the following limit:

\[ \lim_{n\to\infty} \left( 1 - \left( 1 - \frac{1}{n}\right)^{n}\right) \quad = \quad 1 - \frac{1}{e} \quad = \quad 0.63212055... \]

Public key encryption: a quicky in diagrams

Thursday May 9 2024

TLDR: I explain public key (asymmetric) encryption using string diagrams. For the standard references, read New directions in cryptography by Diffe and Hellman (1976).

In symmetric key encryption you have 3 types of data:

• \(X\) of plaintext (unencrypted) messages,
• \(Y\) of ciphertext (encypted) messages,
• \(K\) of keys,

and two one-way functions,

• \(e: X \times K \to Y\), the encryption algorithm or cipher,
• \(d: Y \times K \to X\), the decryption algorithm or decipher.

Given a message \(x\) and a key \(k\), one computes the encrypted message \(y = e(x,k)\) and can only recover \(x\) using the same key via \(x = d(y,k)\); that is, they satisfy

\[ d(e(x, k), k) = x \]

In fact, even stronger, a message encrypted with key \(k\) can only be decrypted using \(k\) again, no other key \(k'\) will work:

\[ d(e(x, k), k') = x \quad \iff \quad k = k', \quad \forall k' \]

The symmetric communication protocol goes like this: Alex wants to send a message \(x\) to Blair, and we assume they both know the key \(k\) beforehand. Alex computes the ciphertext \(y = e(x, k)\) and sends it across the channel. Blair receives the ciphertext and recovers the plaintext via \(x = d(y, k)\). Simple! Here is a diagram showing which parties observe which data:

Notice how the communication channel (highlighted in red) only sees the ciphertext \(y\), and not the plaintext \(x\) nor the key \(k\).

On the other hand, asymmetric encryption like RSA and ECC does not assume Alex and Blair share the key \(k\) beforehand. In this scenario, we have four data types:

• \(X\), \(Y\), and \(K\) as before,
• \(P\), a set of public keys

and three one-way functions:

• \(p: K \to P\) which computes a public key from a private key,
• \(e: X \times P \to Y\), a cipher which takes the message and a public key as input and yields a ciphertext,
• \(d: Y \times K \to X\), the decipher which takes the encrypted ciphertext and a private key and yields the decrypted plaintext.

If \(k\) is a private key and \(p=p(k)\) is the corresponding public key, then \[ d(e(x, p(k)), k) = x \] In fact, even stronger as before: \[ d(e(x, p(k)), k') = x \quad \iff \quad k = k', \quad \forall k' \]

The asymmetric communication protocol now goes like this: Alex wants to send a message \(x\) to Blair, but they don’t share a private key. So, Blair takes their private key \(k\) and generates their public key \(p = p(k)\), then sends it across the channel to Alex. Alex then computes \(y = e(x, p)\) and returns the encrypted message back across the channel to Blair, who then recovers the original message via \(x = d(y, k)\).

As before, notice how the channel only sees the ciphertext and Blair’s public key, but not the original message nor Blair’s private key \(k\); furthermore, Alex never sees Blair’s private key either!

Of course, I never described how any such one-way functions with the above properties could be constructed. That’s where all the prime number bullshit comes in!

AI therapy

Monday May 6 2024

Is AI therapy possible? is it useful? is it ethical? stay tuned!

2020s vibes

Thursday May 2 2024

Just had this weird vision before bed. I’m in my parents’ house in late spring and the temperature soars unpredictably past the highest summer high, past the low 100s, and we can feel it thick in the air. But instead of relief the AC breaks and the tap water dries up, and instead of being saved the groceries are emptied and the roads become clogged. So we sluggishly wait for it to end but it doesn’t.

Self-convincing

Wednesday May 1 2024

My birthday is in a few days!

Anyway, I have done a lot of self-convincing that my failing PhD program was actually good for me, because now I can do something practical.

The reality is the job market for that practical something is fucked, and I don’t have the network or background to enter it. Any person giving advice in this situation says to further your education - whoops!

I’ve also realized that any startup or generative AI idea I have will be had by Ivy league graduates with 10x more friends and 100x more influence and potential than me. So, I seem to have condemned myself to Walmart or Uber, jobs for the antisocial autist which I would have been except for my privilege. 🤠🔫⚡🐜🌼

Pointlessness

Monday April 29 2024

Since failing graduate program and probably no longer to enter that career, main emotion is pointlessness and lack of purpose.

What are language models good for?

Sunday April 28 2024

What are language models even good for? TODO

Panic relief

Sunday April 28 2024

Anxiety! Panic! a cruel dictator that often rule and ruin my life. Here are my coping strategies:

1. Understand and avoid short-term triggers. Mine include (TW) any mention of the heart, heartrate, pulse, or diseases related to the blood or heart.

2. Understand and avoid medium-term causes. For me this includes more than 1 cup of coffee per day, and skipping SSRI medication.

3. Recognize panic symptoms. For me are psychosomatic chest pain (random pain spikes, dull chest aches) and shortness of breath and unsatisfying breaths. Your mind can exaggerate pain and only notice pain near your area of concern (e.g. chest). Another one is jaw pain in the TMJ muscle from grinding or clenching, which may occur unconsciously during anxious sleep. Since often occur to me at night, I become acutely aware no urgent care center is open.

4. Relax muscles and perform breathing exercises. The shortness of breath often comes from unconscious tension in the chest, so relax your chest. A normal unstrained breath should raise and lower the stomach, not the chest. My preferred exercise is 4 seconds each on in/hold/out/hold. Try listening to a youtube video guide or asmr. For nighttime clenching, consider a mouth guard.

5. In last resort, immediate relief drugs. The main one are alprazolam (Xanax), lorazepam (Ativan), and diazepam (Valium). I have heard of beta blockers but they seem less relevant.

6. Accept precarity of life and appreciate its absurd beauty. If you can read this, you already made it far: you are human, you are alive and with vision or e-reader and have internet access. Life owes us nothing, and we can’t obsess over every possible misfortune or else lose the human spirit.

Cyberattacks!

Friday April 26 2024

TODO

Grad school illusion

Thursday April 18 2024

Solar eclipse seems to change peoples minds like at the battle of the eclipse. My friend quit his job. So what perspective change did it cause in me?

I start graduate school in Fall 23. Went about awful as possible, turned into agoraphobic wreck, dropped all correspondence and failed it all. So I’m back home living in the attic.

I was in a mindset where research was the only way for my humanity to matter and the only way to contribute to society. This seems noble but is actually self-centered and covertly narcissistic. It allows no failure and attributes no importance to people outside academia.

Simple flow kick system

Wednesday April 10 2024

In this post I analyze a toy hybrid dynamical system called a “flow-kick” system, which alternates between continuous-time (flow) and discrete-time (kick) dynamics. Here is an example of a time series plot of such a system which alternates between exponential growth and a constant negative kick from Quantifying resilience to recurrent ecosystem disturbances using flow-kick dynamics (2018):

You could imagine they are wildlife that grow in population naturally at some rate \(r\), and you want to harvest/cull them at some fixed amount \(k\) at a fixed annual frequency such that their population remains stable (the orange line). Another example is like, compound interest with interest rate \(r\) on which you make constant payments of amount \(k\), and you want to eventually pay it off (the red line).

A trajectory \(x(t)\) for this system satisfies:

1. \(\frac{d}{dt}x(t) = f(x(t))\) for all \(t \notin \mathbb{Z}\), where \(f(x)=rx\),
2. \(g(x^-(t)) = x^+(t)\) for all \(t \in \mathbb{Z}\), where \(g(x)=x+k\).

where \(\mathbb{Z} = \{...,-2,1,0,1,2,...\}\) is the set of integers, the discrete timepoints where the system undergoes a kick, assumed to have unit spacing. In general we could replace \(f\) and \(g\) with some other flow and kick functions respectively. This is almost enough to specify a unique solution, except we haven’t said whether \(x(t)\) should be equal to \(x^+(t)\) or \(x^-(t)\) whenever \(t\) is at a kick point. To resolve this ambiguity, we can choose the former option by adding a third condition,

3. \(x(t)\) is right-continuous

Ignoring kicks, the solution to the differential equation above is \(x(t) = x(0) e^{rt}\). Setting \(t=1\), we find \(x(1)=x(0) e^r\). Therefore the flow step really just multiples by the constant \(e^r\). It follows that

\[ x(t+1) = x(t) e^r - k \]

for all \(t \in \mathbb{Z}\). This is a non-homogeneous recurrence relation. If we set \(x^*=x(t+1)=x(t)\), we can find the fixed point

\[ x^* = \frac{k}{e^r-1} \]

This is an unstable fixed point above which the solution grows without bound, and below which the solution goes to negative infinity, or more realistically, to zero, in which case you might instead use the kick function \(g(x) = \min\{x-k,0\}\).

All stories are stories about people

Friday April 5 2024

“All stories are stories about people”.

Remind me to update this post whenever I figure out who came up with this concept first.

Some scifi stories are about automation and the rise of machines, at least on the surface. But they really speak about capitalist human relations between worker and owner.

Similarly stories about disaster are not really about the disaster itself, but about the people you fear to lose.

People are the atoms of our lives, not physical atoms - we had to discover those.

Notes on percolation

Sunday March 31 2024

What is “percolation” on a network? Edit: I change my mind let’s call them graphs not networks. For an overview, we can check Wikipedia. For some more details, we can read Percolation and Random Graphs by Remco van der Hofstad. Let me summarize what I found:

1. Percolation on an infinite lattice

• The methods in this first section only apply to infinite lattices, which are infinite graphs with some repeating symmetry. The simplest example is the integer lattice \(\mathbb{Z}^d\) of dimension \(d\). When \(d=2\), it is the infinite chessboard, when \(d=3\), it is Minecraft, etc. Every node \(x \in \mathbb{Z}^d\) is connected to \(2d\) neighbors, left/right, up/down, etc… for each dimension.

• For a given fixed number \(p \in [0,1]\), the “connection probability”, we imagine all the edges in \(\mathbb{Z}^d\) are “enabled” (independently) with probability \(p\) and “disabled” otherwise. We can now ask, for a given \(p\), what is the probability there is an unbroken path between two given nodes? Whatever it is, it should correlate with \(p\), and be equal to \(p\) in the extreme cases \(p=0\) and \(p=1\).

• Given a node \(x \in \mathbb{Z}^d\), let \(C(x)\) be the “cluster” of \(x\), the set of nodes connected to \(x\) by some path. These clusters form a unique partition of space into connected components. When \(p=0\), no edges are enabled, so \(C(x)\) is just \(x\) by itself with probability 1. When \(p=1\), then \(C(x)=\mathbb{Z}^d\), the whole lattice, with probability 1.

• Now we ask, what happens in the intermediate cases when \(p \in (0,1)\)? To answer, we can investigate when the clusters are likely to be finite in size, like when \(p=0\), and when they are likely to be infinite in size, like when \(p=1\). An application of Kolmgorov zero-one law says there must exist a number \(p_c \in [0,1]\) called the critical value, or the phase transition point, such that when \(p<p_c\), every cluster is finite with probability 1, and when \(p>p_c\) then every cluster is infinite with probability 1. (In the latter case, there is only 1 infinite cluster, as any infinite cluster must be unique, since they are bound to unite at some point.)

  • In case it’s not clear what an “infinite cluster” means, you can also choose some large number \(R>0\) and calculate the probability of a path from the origin in \(\mathbb{Z}^d\) to the edges of the \(d\)-dimensional bounding box \([-R,R]^d\), and take the limit as \(R \to \infty\).
  • We say “every cluster” because the lattice is homogeneous, so every node will share the same qualitative properties such as infinite cluster probability.
  • In the case that \(p_c=0\) or \(1\) the phase transition is called trivial.

• When \(d=2\), Kesten (1982) showed \(p_c=\frac{1}{2}\). In other words if more than 50% of edges are enabled on the infinite chessboard, an unbroken path to infinity is guaranteed… weird! For other values of \(d\), and other types of lattices, it is rare to find the exact value of \(p_c\). Another known case is an \(r\)-regular tree has \(p_c=\frac{1}{1-r}\).

• We can sometimes bound the critical value: on \(\mathbb{Z}^d\), if \(d \geq 2\), then \(\frac{1}{2d-1} \leq p_c < 1\), which guarantees it is non-trivial. If the graph is transitive with degree \(r\), then \(\frac{1}{r-1} \leq p_c\).

2. Finite graphs

• Let \(G\) be a undirected graph and let \(V\) be the set of nodes, with \(|V|=n\). The degree of a node \(x \in X\) is the number of other nodes connected to \(x\). We can define

  • the degree sequence \(D_0,D_1,D_2,\cdots\) where \(D_k\) is the number of nodes with degree \(k\). It follows that \(\sum_{k=0}^{\infty}D_k=n\), and also \(D_k\) must be zero eventually.
  • the degree distribution \(d_0,d_1,d_2,\cdots\) which is just \(d_i = \frac{D_i}{n}\). It turns the degree sequence into a probability distribution with \(\sum_{k=0}^{\infty} d_k=1\)

• A scale-free graph is one that has a power-law degree distribution, \(d_k \sim k^q\) for some exponent \(q\). This is not a precise definition for finite graphs (and hence real world networks), but can be checked in practice by doing linear fit to the loglog equation \(\log(d_k) = a_0 + a_1 \log(k)\).

• A graph is clustered if for any nodes \(x,y,z\), an edge between \(x,y\) and an edge between \(x,z\) often imply an edge between \(y,z\), that is, more than would be expected at random. One can define the clustering coefficient \(C\) of a graph based on the preceding principle using a big equation I won’t repeat here. A typical unclustered graph satisfies \(C=C_0=\frac{2|E|}{n(n-1)}\), where \(|E|\) is the number of edges. Thus a graph is considered clustered when \(C\) is much greater than \(C_0\).

• A small-world graph is one where the distance between nodes is relatively small, like the Kevin Bacon or Erdos number thing (defined more precisely later).

3. Random graph processes

• Let \(G_t=\{G_t \mid t =0,1,2,\cdots \}\) be a sequence of graphs, called a graph process.

• Given a graph process \(G_t\) let \(d_{k,t}\) be the degree distribution at step \(t\). The process is called sparse if there exists a limiting degree distribution \(d_k\) such that \(\lim_{t\to\infty} d_{k,t}=d_k\).

• A sparse graph process \(G_t\) with limiting degree distribution \(d_k\) is called scale-free if there exists some \(\tau\) such that \(\lim_{k\to\infty} \frac{\log(d_k)}{\log(1/k)} = \tau\).

• The graph process is called highly clustered if \(\lim_{t\to\infty} C_t > 0\), where \(C_t\) is the clustering coefficient at step \(t\).

• The graph process is small-world if, given the measurement \(H_t\) of “average distance” between nodes in \(G_t\) so-defined, then \(\lim_{t\to\infty} \text{Prob} (H_t \leq K \log t) = 1\) for some constant \(K\).

4. Some examples

• He introduces a class of models calls inhomogeneous random graphs.

  • This includes as a special case the well known Erdos-Renyi graph, considered as a graph process where \(t=0,1,2,...\) is the number of nodes and \(p = \frac{\lambda}{t}\), for some fixed number \(\lambda\). The limiting degree distribution of this process is \(d_k = \frac{e^{-\lambda} \lambda^k}{k!}\), a Poisson distribution with parameter \(\lambda\), so it is sparse but not scale-free.

• Next introduces the preferential attachment (Barabási–Albert) model, where new nodes are introduced at each step and attach to existing nodes with more edges with higher probability. It is a scale-free graph process with the power law \(d_k \sim k^{-3}\), and hence an interesting case study of the precending theories.

• So far we considered percolation on infinite graphs, properties of finite graphs and graph processes. So how do we unify the two, and model percolation on finite random graph processes? Unfortunately, the remaining parts which explain this (Theorem 1.17 in Section 1.3.3 and onward) go above above my head…

Dijkstra’s generalized pigeonhole principle for bags

Friday March 22 2024

Pigeonhole principle is a theorem in mathematics that says, in plain language: if you release a flock of pigeons into a pigeon coop, and every pigeon flies into a pigeonhole, and the number of pigeons is greater than the number of pigeonholes, then there must be at least one pigeonhole containing more than 1 pigeon.

Apparently Dijkstra thought this version was too weak, and wrote “The undeserved status of the pigeon-hole principle” in 1991 where he states his preferred version:

for a nonempty, finite bag of real numbers, the maximum is at least the average, and the minimum is at most the average.

Note he did not say finite set of real numbers. Instead, by “bag” he means a multiset, or unordered list, a set where repeats are allowed (see: Why does mathematical convention deal so ineptly with multisets?)

But how does this version generalize the original? The idea is that we define the multiset \(S\) to be the “census” of pigeonboxes of each possible size. In the example pictured above, we would have \(S=\{2,1,1,1,1,1,1,1,1\}\), where the minimum is 1, the maximum is 2, and the average is 10/9. Dijkstra’s theorem correctly says \(1 \leq 10/9 \leq 2\).

Let’s now prove that Dijkstra’s principle is indeed stronger, i.e. that it implies the original principle. First let’s clearly state each.

Pigeonhole principle version 1: Let \(A\) and \(B\) be finite sets, and let \(f:A \to B\) be a function, assigning each \(a \in A\) to \(f(a) \in B\). For each \(b \in B\), let \(n(b)\) be the number of elements of \(A\) that are assigned to \(b\). If \(|A|>|B|\) (\(A\) has more elements than \(B\)) then there must exist some \(b \in B\) such that \(n(b)>1\).

Pigeonhole principle version 2 (Dijkstra): Let \(S\) be a finite multiset of real numbers. Then \(\mathrm{minimum}(S) \leq \mathrm{average}(S) \leq \mathrm{maximum}(S)\).

Proof v2 ⇒ v1: Let \(f: A \to B\) be a function between finite sets and assume \(|A|>|B|\). We want to use Dijkstra’s principle to prove there exists \(b \in B\) such that \(n(b)>1\). Define the multiset \(S = \{ n(b) \mid b \in B\}\). Observe that the average of \(S\) is equal to the ratio of the sizes of the two sets:

\[ \mathrm{average}(S) = \frac{\sum_{b \in B} n(b)}{|B|} = \frac{|A|}{|B|} \]

Since we assumed \(|A| > |B|\), this ratio is greater than 1:

\[ \mathrm{average}(S) = \frac{|A|}{|B|} > 1 \]

Combining this with Dijkstra’s principle, \[ \mathrm{maximum}(S) \geq \mathrm{average}(S) > 1 \] Therefore \[ \mathrm{maximum}(S) > 1 \] This means \(S\) contains a number larger than 1, which corresponds to an element \(b\) with \(n(b)>1\), so that completes the proof!

Multicellularity

Wednesday March 20 2024

Humans are made of cells, and societies are made of humans. Are we, like, cells in a “social organism”?

Some references to find out include:

• The major transitions in evolution (1995) by John Maynard Smith (author of Evolution and the Theory of Games (1982)) and Szathmáry.

• Major evolutionary transitions in individuality (2015) gives some necessary conditions: “cooperation, division of labor, communication, mutual dependence, and negligible within-group conflict”.

• Ecological scaffolding and the evolution of individuality (2020) by Rainer, Bourrat et al. Includes a mathematical model.

• The information theory of individuality (2020) by Krakauer, Flack, et al.

• Some other keywords include: group agents, collective agency, enactive theory of agency, sense-making, bio-semiosis, ontologies of organismic worlds

Why does gimbal lock happen?

Wednesday March 13 2024

Quick, explain gimbal lock! 🌐

When you represent rotations by 3 numbers, the Euler angles, this corresponds to a map \(f:T^3 \to RP^3\) from the 3-dimensional torus to the 3-dimensional real projective space, regarded as differentiable manifolds. It can be proven that any such map cannot be a covering map ands a result at some points of the domain the map has a rank of 2, rather than 3. Those are the points where the gimbal lock occurs.

Vakil’s easy exercise

Wednesday March 13 2024

Here is “easy exercise” #11.1.A from Vakil about the spectrum of a commutative ring:

Show that \(\mathrm{dim} \, \mathrm{Spec} \, R = \dim \, R\)

Um… I at least think that the left side refers to the topological dimension and the right refers to the Krull dimension.

Reversible subsystem

Wednesday March 13 2024

Let \(X\) be a set and \(f:\mathbb{N}\times X \to X\) be a monoid action of the natural numbers on \(X\), an irreversible discrete-time dynamical system. Let \(P = \{ x \in X \mid \exists n\neq 0, f(n,x)=x \}\) be the set of periodic points, and let \(p:P \to \mathbb{N} - \{ 0 \}\) be a function assigning each points to its period. Then we can extend the monoid action \(f\) restricted to \(P\) to a group action \(g:\mathbb{Z} \times P \to P\) via

\[g(t, x) := f(t\bmod p(x),x)\]

This seems to be the “maximal reversible subsystem” (reference request) because the following diagram commutes, where \(i:\mathbb{N} \to \mathbb{Z}\) and \(j:P \to X\) are inclusions:

              ℕ × j
     ℕ × P  ————————▶  ℕ × X
       │                 │
 i × P │                 │ f
       ▼                 ▼
     ℤ × P  ——▶  P  ——▶  X
             g       j

Particle collision in cellular automata

Tuesday March 12 2024

Cellular automata are cool! They exhibit lots of emergent phenomenon like “particles” aka “gliders”. A particle is roughly defined as any finite configuration of cells that repeats after some fixed number of steps, displaced by some amount. That is, each particle has a period \(p\) (a natural number) and a displacement vector \(d\) which, for cellular automata on an integer grid, will be an integer vector. The “velocity” of the particle is then given by \(d/p\), a real-valued vector.

For extensive reading on this topic check out Solitons and particles in cellular automata: a bibliography by Steiglitz (1998).

What’s even more interesting is these particles can interact via collision and create new particles! For example the people on Game of Life wiki categorized all 71 possible glider collisions. Particle collision also played an important role in Matthew Cook’s proof that Rule 110 is a universal Turing machine. Here are all the particles in Rule 110:

Here is an interesting theorem about particle collision proved in Soliton-like behavior in automata by Park, Steiglitz, and Thurston (1986): suppose you have a cellular automata on the 1-dimensional integer lattice (such as the elementary cellular automata) and two particles. Suppose the first particle has a period of \(p_1\) and a displacement of \(d_1\) cells, and the second has period \(p_2\) and displacement \(d_2\). Assume \(\frac{d_1}{p_1} \neq \frac{d_2}{p_2}\) (they have different velocities) since otherwise they can never collide. Then the maximum number of possible outcomes of their collision is \(p_1 \cdot p_2 \cdot (d_2-d_1)\).

This theorem is generalized to higher dimensions in Upper bound on the products of particle interactions in cellular automata by Hordijk, Shalizi, Crutchfield (2000).

To formally define a particle in a cellular automaton, first need to define cellular automata. A cellular automata consists of

• a set \(X\) of “points” or “cells” equipped with a transitive group action (the translation group) such as \(X=\mathbb{Z}^D\), the \(D\)-dimensional integer lattice,
• a set \(Y\) whose elements are called cell states or local states,
• a function \(F: (X \to Y) \to (X \to Y)\), where each function \(u:X \to Y\) is called field configurations or global states or something, and \(F\) must obey…
• \(F\) is translation-equivariant
  • this means \(FT[u]=TF[u]\) for every \(u:X \to Y\) and every translation \(T\).
• \(F\) is a local rule, meaning \(F[u](x)\) only depends on \(u\) in some neighborhood \(N_x \subseteq X\) of \(x\).
  • assuming translation equivariance we could equivalently define some universal neighborhood \(N\) as a subset of the translation group so that \(N_x=N+x\).
  • by the Curtis–Hedlund–Lyndon theorem you could replace this with the assumption \(F\) is continuous in the so-called “prodiscrete topology” on \(U\).

In order to define a particle-like solution, it needs to be “localized” in some way, and so you need to choose some background state. A particle with respect to a background \(0_Y \in Y\) is then a configuration \(u\) such that

• \(\{ x \in X \mid u(x) \neq 0_Y \}\) is a finite set
• there exists \(p \geq 1\) and a displacement \(d \in \mathbb{Z}^D\) such that such that \(F^p[u] = T^d[u]\), where \(T^d\) denotes translation action of \(d\),
• possibly some secret third property that says it can’t be decomposed into smaller disjoint particles

If \(u\) is finite and \(F\) is a local rule then \(F[u]\) is also finite, so finiteness is a forward time-invariant property. The second condition says after \(p\) steps the spot returns to its original configuration with some displacement. If \(d\) is the corresponding displacement element then the spot moves with average velocity \(v = \frac{d}{p}\).

Wall collision. In one dimension, when \(X = \mathbb{Z}\), another type of localized solution are traveling fronts which connect two different equilibria. These are only localized in one-dimension; in general they form a boundary between two regions of space and are \((D-1)\)-dimensional. In physics they are called domain walls. Let’s also call them walls: define a (1D periodic traveling) wall to be a configuration \(u: \mathbb{Z}^1 \to Y\) such that

• there exists \(p \in \mathbb{N}\) and \(d \in X\) such that \(F^p[u] = T^d[u]\).

• there exist points \(x_L,x_R \in \mathbb{Z}\) such that \(u\) is constant on \((-\infty,x_L]\) and \([x_R,\infty)\).

Returning to the Rule 184 example, it said on Wikipedia he classified all the collisions, but I don’t actually see that, so let’s do it ourselves. The previous theorem seems to suggest an upper bound of 8 or 16 outcomes depending on the interactants, which is clearly an overestimate because the interactions all have unique outcomes - let’s have a look! Mind the notation: 0s and 1s denote cells that are in the body of a spot while . and , denote background 0s and 1s. Just based on the signs of the velocities alone we can determine there are 5 possible collisions:

1. \(\gamma^+ \otimes \gamma^- \to *\), annihilation to the alternating background:

00,.,.,.11
,00,.,.11.
.,00,.11.,
,.,0011.,.
.,.,.,.,.,
,.,.,.,.,.
.,.,.,.,.,

2. \(\gamma^+ \otimes \alpha^- \to \alpha^-\)

,00,.,.,01
.,00,.,01,
..,00,01,,
.,.,011,,,
,.,01,,,,,
.,01,,,,,,
,01,,,,,,,

3. \(\omega^+ \otimes \gamma^- \to \omega^+\) mirrors the previous case

01.,.,.11.
.01.,.11.,
..01.11.,.
...011.,.,
.....01.,.
......01.,
.......01.

4. \(\alpha^+ \otimes \beta \to \alpha^-\)

10...01,,
.10..01,,
,.10.01,,
.,.1001,,
,.,.10,,,
.,.10,,,,
,.10,,,,,
.10,,,,,,

4. \(\beta \otimes \omega^- \to \omega^+\) mirrors previous case

..01,,,10
..01,,10,
..01,10,.
..0110,.,
..010,.,.
...01.,.,
....01.,.
.....01.,
......01.

5. \(\omega^+ \otimes \alpha^- \to \beta\)

01.,.,.,01
.01.,.,01,
..01.,01,,
...0101,,,
....01,,,,
....01,,,,
....01,,,,

Returning to the \(D\)-dimensional system, note that even though the system is non-reversible, we can extend to a reversible system on spots. Let \(P \subseteq U\) be the subset of spot configurations and let \(p:P \to \mathbb{N}\) assign each spot its period. Then we can extend \(F^t\) to an action on \(P\) for all \(t \in \mathbb{Z}\) via

\[ F^t u_t = F^r T_d^n [u], \quad t = np + r, \quad 0 \leq r < n \]

where \(t = np + r\) is the Euclidean division of \(t\) by \(p\).

Next, given two states \(u_1,u_2 \in U\), define the following commutative binary operation.

\[ (u_1 \oplus u_1)(x) = \begin{cases} u_1(x) & u_2(x) = 0_Y \\ u_2(x) & u_1(x) = 0_Y \\ 0_Y & u_1(x) \neq 0_Y \text{ and } u_2(x) \neq 0_Y \end{cases} \]

Let \(u_1\) and \(u_2\) be two particles with period \(p_i\) and displacement \(d_i\) for \(i=1,2\) and let \(v_i=\frac{d_i}{p_i}\). I don’t know how to prove it, but if \(v_1 \neq v_2\), then there exists \(t_0 \in \mathbb{Z}\) such that \[t \leq t_0 \implies F^t[u_1 \oplus u_2] = F^t[u_1] \oplus F^t[u_2]\] This defines a sequence of states \(u_t\) which is a \(\oplus\) of two incoming particles as \(t \to -\infty\) and which is unconstrained as \(t \to +\infty\).

Reading:

• Ceccherini-Silberstein, Coornaert (2010). Cellular automata and groups
• Pivato (2007). Defect particle kinematics in one-dimensional cellular automata
• Cook (2004). Universality in elementary cellular automata
• Aaronson (2002). Book review: “New Kind of Science”"
• Hordijk, Shalizi, Crutchfield (2000). Upper bound on the products of particle interactions in cellular automata
• Steiglitz (1998) . Solitons and particles in cellular automata: a bibliography
• Das, Mitchell, Crutchfield (1994). A genetic algorithm discovers particle-based computation in cellular automata
• Park, Steiglitz, Thurston (1986). Soliton-like behavior in automata

PS: Reflecting on an earlier post my definition of moving spot was not quite correct, because it doesn’t account for the important case of periodic background. So, how do account for this? A background state is one that satisfies \(F^t[u]=u\) for some \(t\) and \(T^d[u] = u\) for some \(d\). Thus it is periodic in both space and time. If \(u_1\) and \(u_2\) are two background states, then a wall (or wave) connecting them should perhaps be a function \(w\) such that there exist \(x_L\) and \(x_R\) such that \(u_1(x)=w(x)\) for all \(x<x_L\) and \(w(x)=u_2(x)\) for all \(x>x_R\). The set \([x_L,x_R]\) will be called the support of \(w\). Without loss of generality assume \(x_L\) is maximal and \(x_R\) is minimal. Notice if the support of \(w\) is finite and \(F\) is local then so is the support of \(w\). Finally, we can define a moving wall to be such a \(w\) along with \(p\) and \(d\) such that \(F^p[w]=T^d[w]\). More generally you could define a domain wall like this I guess… \(u_1\) and \(u_2\) are two global patterns, \(A_1\) and \(A_2\) are two subsets of space where the state matches \(u_1\) and \(u_2\) respectively, and \((A_1 \cup A_2)^C\) is the domain wall. The problem is how to define interactions in this case? And prove anything about them?

Solipsistic theorem

Thursday March 7 2024

Recently my friend asked my thoughts on dualism vs monism. I had to look up what is the difference. But it made me start thinking about Mealy machines, a mathematical formalization of systems with input, output, and state (memory) - like a computer! They are an even simpler version of the von Neumann architecture. Formally a Mealy machine consists of:

• a set of possible states, \(S\)
• a set of possible inputs, \(I\)
• a set of possible outputs, \(O\)
• a function \(f: S \times I \to S \times O\) called the “update” function which takes the current state value and an input value and yields the next state value and an output value. Here \(\times\) is the Cartesian product of sets.

Given an initial state and a sequence of inputs, a Mealy machine can run autonomously and produce a sequence of outputs. Specifically, given an initial state \(s_0\) and a sequence \(i_0,i_1,i_2,...\) of inputs, the Mealy machine determines a sequence \(s_1,s_2,s_3,\cdots\) of states and \(o_1,o_2,o_3,...\) of outputs using the update function, \((s_{t+1},o_{t+1}) = f(s_t,i_t)\) for each \(t=0,1,2,...\).

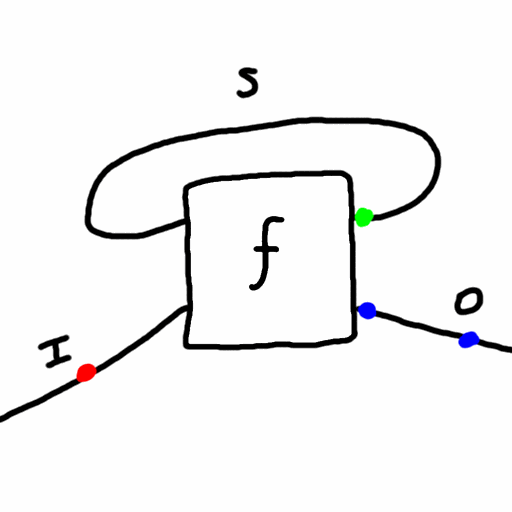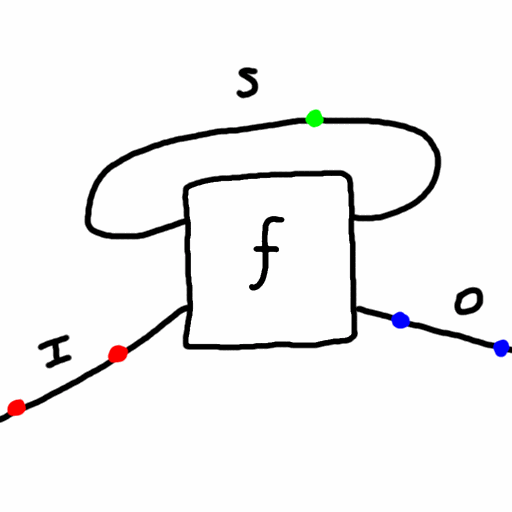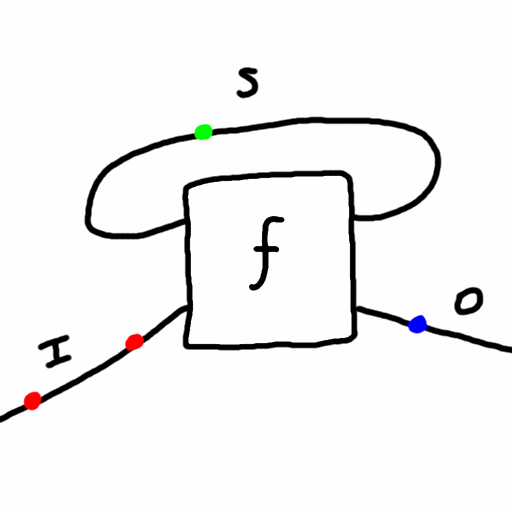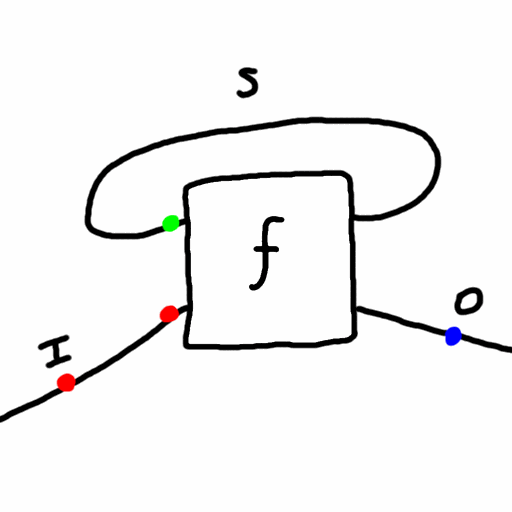
Animation based on this blog post.

In “mind-body dualism” I imagine there are two Mealy machines, hooked up to one another, where one machine is the world, including the body, and other is the mind. We observe our senses, process thoughts, take action. Likewise the world “observes” our action, processes it via physics, and “acts” on us by sending us a new observation in an endless cycle… 🌹🪰😊

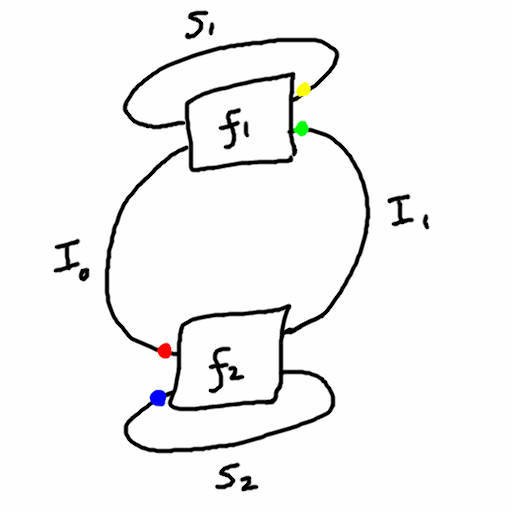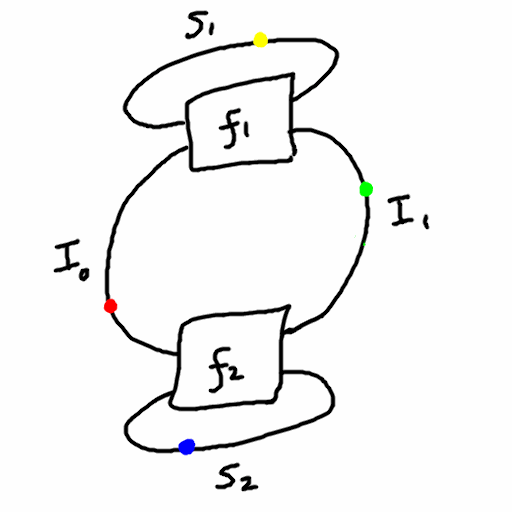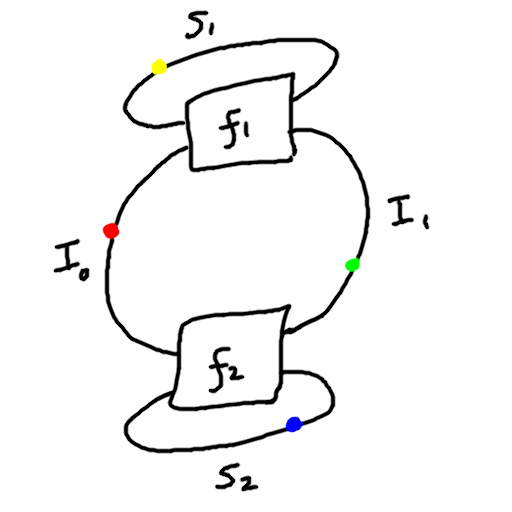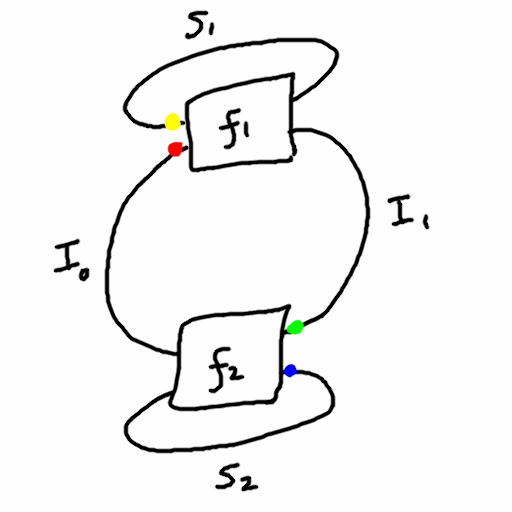
Since there is a symmetry between the agent and environment, with the output of one being the input of the other and vice versa, I will replace the words “input” and “output” with “interface”, and always use capital letter I. So a “dualistic system” consists of

• four sets: \(S_1,S_2,I_1,I_2\)
• two functions:
  • \(f_1: S_1 \times I_1 \to S_1 \times I_2\)
  • \(f_2: S_2 \times I_2 \to S_2 \times I_1\)

Thus, \(S_1\) and \(S_2\) are the state sets of the two machines, and \(I_1\) and \(I_2\) are their “interfaces” (input/output and output/input respectively). This is not unlike a partially observed Markov decision process which are commonly used in reinforcement learning.

Next consider a system with multiple agents: suppose there are \(n\) total. Then we have

• sets \(S_1, S_2^1, ..., S_2^n\) of agent states,
• sets \(I_1^1, ..., I_1^n, I_2^1, ..., I_2^n\) of interfaces,
• functions:
  • \(f_1: S_1 \times \prod_i I_1^i \to S_1 \times \prod_i I_2^i\)
  • \(f_2^i: S_2^i \times I_2^i \to S_2^i \times I_1^i\) for each \(i=1,...,n\)

This is like having one central Mealy machine, the environment, hooked up to a bunch of other Mealy machines, the agents. Similar concepts found in multi-agent reinforcement learning. When \(n=1\), it’s exactly the same as a dualistic system.

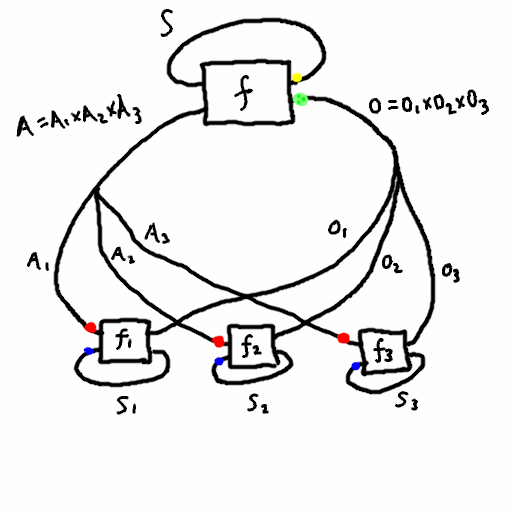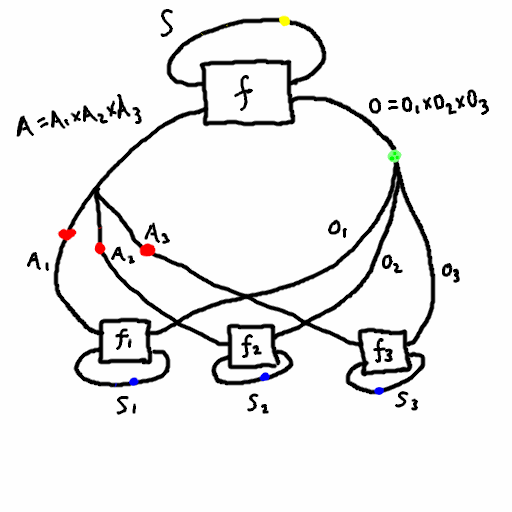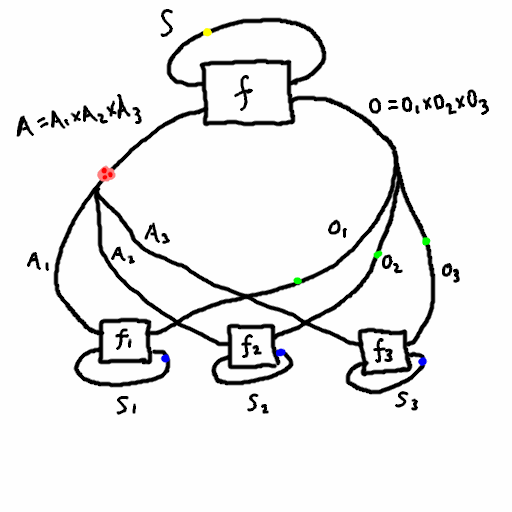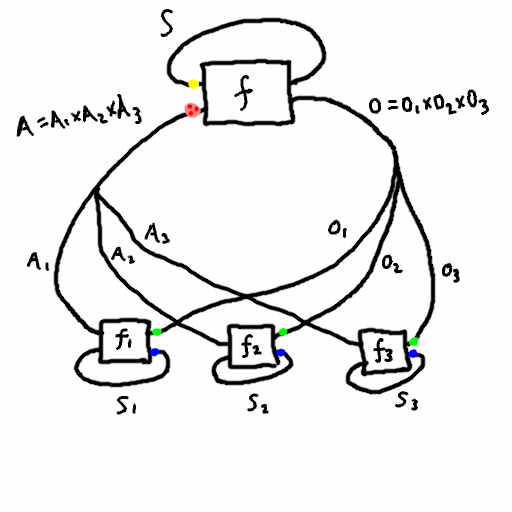
Theorem (informal): any agent in a multi-agent system can view themselves as part of a dualistic system, where all the other agents are part of the environment. See the figure below, where the pink box designates the enlarged environment containing every agent except \(j\), where \(j=1\).

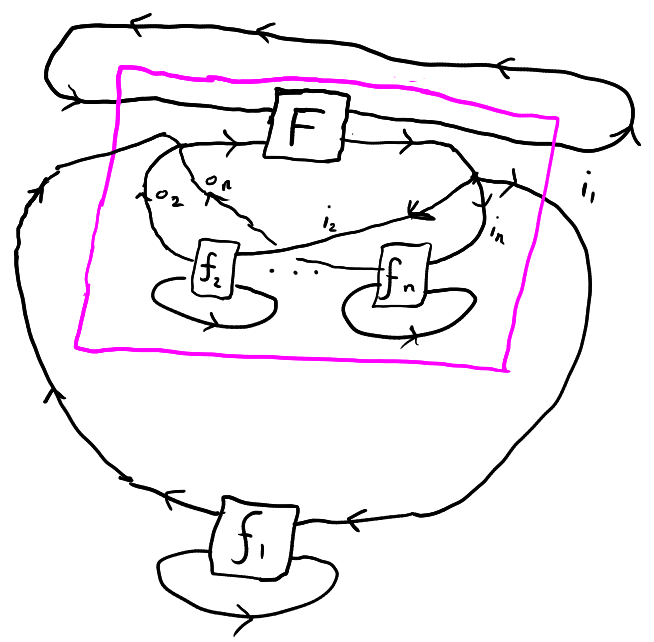
Theorem (more formal): choose an agent \(j\). Then we can turn the multi agent system into a dual system where \(S_1 = S_1 \times \prod_{i \neq j} (S_2^i \times I_1^i \times I_2^i)\), \(S_2 = S_2^j\), \(I_1 = I_1^j\), \(I_2 = I_2^j\), and \(f_2 = f_2^j\). As for \(f_1\), it can be described in psuedo-psuedocode as follows:

• it takes \((s_1, s_2^1, i_1^1,i_2^1, ..., s_2^{j-1}, i_1^{j-1},i_2^{j-1},s_2^{j+1},i_1^{j+1},i_2^{j+1}, ..., s_2^n,i_1^n,i_2^n)\) and \(i_1^j\) as input
• first it combines \(i_1^j\) with all the other \(i_1\)’s along with \(s_1\) and computes \(f_1\), yielding the new \(s_1\) value along with new \(i_2\) values for all the \(n-1\) agents aside from \(j\).
• each agent \(i\neq j\) is given its new \(i_2\) value, combined with its current state \(s_2\), to produce the new \(s_2\) value and the next \(i_1\).
• thus all the state values have been updated, and it sends the output \(i_2^j\) back to agent \(j\).

Todo. Is there any mention of this concept in literature? It sounds like something Douglas Hofstadter](https://en.wikipedia.org/wiki/I_Am_a_Strange_Loop) would say. It reminds me of Cartesian framing. You could express using the language of the polynomial functors book by Spivak as in Example 4.60. But they use Moore machines instead of Mealy machines, which in their language is a lens \(Sy^S \to Oy^I\), so I would have to redo all the animations.

Short tour of dynamical systems

Tuesday March 5 2024

If I had to give a short tour of the mathematical field of dynamical systems, given that I am totally unqualified to do so, what would I say?

It is a very general concept: a dynamical system has a state that changes over time and that’s about it. dynamical systems are everywhere, a swinging pendulum, the planets in the solar system obeying Newton’s laws, indeed the whole universe itself and its physics (with some caveats). But what is state, and what is time? The simplest answer is to let \(X\) be a set of possible states, and let \(f:X \to X\) be a function from \(X\) to itself. Given an initial point \(x_0 : X\), we can generate the sequence \(x_1,x_2,x_3,\cdots\) by applying \(f\) repeatedly, where \(t=0,1,2,3,\cdots\) becomes the time variable. This is the world of discrete dynamical systems, aka iterated maps or recurrence relations, examples including the Fibonacci sequence, Collatz map, and logistic map. One studies fixed points, stable points, periodic points, attractors, period-doubling bifurcation, chaos, bifurcation digrams, the Feiegenbaum constants, bifurcation theory, arithmetic dynamics, complex dynamics like the Mandelbrot set, Sharkovskii’s theorem, Peixoto theorem.

Corollary of Sharkovskii’s theorem: Let \(I \subseteq \mathbb{R}\) be an interval and let \(f:I \to I\) be a continuous function. - if \(f\) has only finitely many periodic points, then they must all have periods that are powers of two - if there is a periodic point of period three, then there are periodic points of all other periods

Usually all that comes much later, after a more practical course in differential equations. In this context, the object under study may not even be a dynamical system by the standard definition, because we first need to show that solutions exist. For that we have Picard’s theorem. Then we can solve linear equations, other special methods, limit cycles, homoclinic and heteroclinic orbits, phase portraits, invariant manifolds, hyperbolic points, (Lyapunov) stability, the Hartman-Grobman theorem.

What is the difference between a differential equation and a dynamical system?

If you allow time to be either discrete or continuous, you might let \(X\) be a set, \(T\) be a monoid (or a group but I prefer monoid, since you don’t have to assume the system is reverseible). Then \(\phi:T \times X \to X\) is a monoid action of \(T\) on \(X\). Some say \(T\) is an arbitrary monoid, but the Handbook of Dynamical Systems requires \(T \subseteq \mathbb{R}\), that is, \(T\) must be a subset (sub-monoid) of the real numbers. If that seems arbitrary recall that \(\mathbb{R}\) is the “unique complete ordered field”. Then you can put additional structure on the state set like giving it a measure, then you get measure-preserving dynamical systems, topological conjugacy and structural stability, ergodic systems and the ergodic theorems, Poincare map and the Poincare recurrence theorem, I got bored and made this desmos animation for Poincare map, Hopf decomposition, Anosov flows, conservative and dissipative systems, symbolic dynamics, [cellular automata[(https://en.wikipedia.org/wiki/Cellular_automaton)], the Curtis–Hedlund–Lyndon theorem, Willems’ behavioral approach to systems theory.

Active research areas in no particular order: linear control, nonlinear control, dynamic programming, stochastic processes, random walks, stochastic PDEs, dynamical billiards seems pointless, integrable systems, PDEs, topological dynamics, nonlinear waves, fluid dynamics, holomorphic dynamics, dynamical zeta functions aka Ruelle zeta function, twist maps and Moser’s twist theorem (I assume they’re related), low-dimensional dynamics, Floer homology, renormalization group, traveling waves, algebraic dynamics, coupled oscillators, phase-locking, singular perturbation theory, conley index, blow-up phemenon, cocycles, cohomology, Oseledets theorem, blogpost by Terenace Tao, moduli space, Kupka-Smale theorem, Pugh’s closing lemma, Smale’s problems, Morse–Smale system, catastrophe theory, singularity theory, pattern formation, synchronization, applied category theory, Koopman theory, percolation, nonlocal interaction terms, higher order interaction, delay.

Open problems? Hilbert 16th problem is still open, Boltzmann–Sinai ergodic hypothesis was resolved recently TODO more here. Also todo more HISTORY.

More sections: PDE

Dynamical systems tour

Tuesday March 5 2024

How would I give a tour of the mathematical field of dynamical systems given that I am totally unqualified to do so?

It is a very general concept: a dynamical system has a state that changes over time and that’s about it. dynamical systems are everywhere, a swinging pendulum, the planets in the solar system obeying Newton’s laws, indeed the whole universe itself and its physics (with some caveats). But what is state, and what is time? The simplest answer is to let \(X\) be a set of possible states, and let \(f:X \to X\) be a function from \(X\) to itself. Given an initial point \(x_0 : X\), we can generate the sequence \(x_1,x_2,x_3,\cdots\) by applying \(f\) repeatedly, where \(t=0,1,2,3,\cdots\) becomes the time variable. This is the world of discrete dynamical systems, aka iterated maps or recurrence relations, examples including the Fibonacci sequence, Collatz map, and logistic map. One studies fixed points, stable points, periodic points, attractors, period-doubling bifurcation, chaos, bifurcation digrams, the Feiegenbaum constants, bifurcation theory, arithmetic dynamics, complex dynamics like the Mandelbrot set, Sharkovskii’s theorem, Peixoto theorem.

Usually all that comes much later, after a more practical course in differential equations. In this context, the object under study may not even be a dynamical system by the standard definition, because we first need to show that solutions exist. For that we have Picard’s theorem. Then we can solve linear equations, other special methods, limit cycles, homoclinic and heteroclinic orbits, phase portraits, invariant manifolds, hyperbolic points, (Lyapunov) stability, the Hartman-Grobman theorem.

If you allow time to be either discrete or continuous, you might let \(X\) be a set, \(T\) be a monoid (or a group but I prefer monoid, since you don’t have to assume the system is reverseible). Then \(\phi:T \times X \to X\) is a monoid action of \(T\) on \(X\). Some say \(T\) is an arbitrary monoid, but the Handbook of Dynamical Systems requires \(T \subseteq \mathbb{R}\), that is, \(T\) must be a subset (sub-monoid) of the real numbers. If that seems arbitrary recall that \(\mathbb{R}\) is the “unique complete ordered field”. Then you can put additional structure on the state set like giving it a measure, then you get measure-preserving dynamical systems, topological conjugacy and structural stability, ergodic systems and the ergodic theorems, Poincare map and the Poincare recurrence theorem, I got bored and made this desmos animation for Poincare map, Hopf decomposition, Anosov flows, conservative and dissipative systems, symbolic dynamics, [cellular automata[(https://en.wikipedia.org/wiki/Cellular_automaton)], the Curtis–Hedlund–Lyndon theorem, Willems’ behavioral approach to systems theory.

Active research areas in no particular order: linear control, nonlinear control, dynamic programming, stochastic processes, random walks, stochastic PDEs, dynamical billiards seems pointless, integrable systems, PDEs, topological dynamics, nonlinear waves, fluid dynamics, holomorphic dynamics, dynamical zeta functions aka Ruelle zeta function, twist maps and Moser’s twist theorem (I assume they’re related), low-dimensional dynamics, Floer homology, renormalization group, traveling waves, algebraic dynamics, coupled oscillators, phase-locking, singular perturbation theory, conley index, blow-up phemenon, cocycles, cohomology, Oseledets theorem, blogpost by Terenace Tao, moduli space, Kupka-Smale theorem, Pugh’s closing lemma, Smale’s problems, Morse–Smale system, catastrophe theory, singularity theory, pattern formation, synchronization, applied category theory, Koopman theory, percolation, nonlocal interaction terms, higher order interaction, delay equations.

4 types of categories to know about

Thursday February 29 2024

If you wish to know more about category theory, then the following 4 types may become of importance to you:

1. Concrete categories are ones where, roughly speaking, the objects are sets with some additional structure. Many objects in mathematics, like fields, vector spaces, groups, rings, and topological spaces, can be represented this way. For a detailed list of examples check out Example 1.1.3 in Category Theory in Context (free pdf). For example, if X is a topological space, then X would be an object in the category of topological spaces. Now, every topological space has an underlying set of points. This is represented by the forgetful functor from the category of topological spaces to the category of sets, sometimes denoted \(U:\mathrm{Top} \to \mathrm{Set}\). In that case \(U(X)\) would be the underlying set of points of \(X\).

2. Monoidal categories. Many categories have a way to combine two objects, like the Cartesian product \(A \times B\) of sets, the direct product of two groups, the tensor product of two vector spaces, etc, that constitute a binary operation. Furthermore in each case there is a unit object which serves as an identity for the binary operation: the singleton set (with one element), the trivial vector space (with one point), etc. This is the premise of a monoidal category. Insert segue into Rosetta stone paper here.

3. Cartesian closed categories. This type of category is commonly used to represent the type systems within some programming languages. Given two objects \(A\) and \(B\) in a “CCC”, you can form the product \(A \times B\) as well as the exponential \(B^A\), also written more suggestively as \(A \to B\). When \(A\) and \(B\) are sets (or types) then \(B^A\) can be understood as the set (type) of functions (or “programs”) from \(A\) to \(B\). If you combine this with point 2, so that the product \(\times\) obeys the monoidal laws, then you get a closed monoidal category. I need a better reference on this.

4. Abelian categories. If you ever try to study algebraic topology you will come across the concept of homology (or cohomology) and the notion of a chain complex. Let \(Ab\) be the category of abelian groups (which is a concrete category as well as a monoidal category). A chain complex of abelian groups is a sequence \(A_0, A_1, A_2, \cdots\) of abelian groups, along with homomorphisms \(d_n: A_{n+1} \to A_n\) for each \(n\), such that \(d_{n} \circ d_{n+1} = 0\) for all \(n\), where on the left is the composition of \(d_{n+1}\) with \(d_n\) and on the right is the zero morphism from \(A_{n+2}\) to \(A_n\), which sends every element to zero. If one asks, “what is the most general category I can replace \(Ab\) with?” the answer would be one where you have zero morphisms, and a few other things… anyway, people already figured this out, and they are called abelian categories!

Autoprovers > autoformalizers?

Wednesday February 28 2024

Autoformalization is a way to encode all the mathematical work that’s already been done by inputting the pdfs or latex files into a computer and asking it to parse out all the little details into a completely rigorous, type-checked proof.

But what if it’s easier to just redo all the work from scratch? This is the basic premise of automated theorem proving. Let’s go with the following dubious logic: if there was some amazing method to automatically prove theorems without advances in deep learning, then they would have already been found. Therefore it suffices to look at automated theorem proving in the context of neural theorem provers specifically.

Alright! Let’s first look at GPT-\(f\) from 2 people at OpenAI.

Here’s a list of some neural theorem provers:

• Stanislas Polu and Ilya Sutskever. Generative language modeling for automated theorem proving. arXiv preprint arXiv:2009.03393, 2020

Jesse Michael Han, Jason Rute, Yuhuai Wu, Edward W Ayers, and Stanislas Polu. Proof artifact co-training for theorem proving with language models. arXiv preprint arXiv:2102.06203, 2021. [18] Stanislas Polu, Jesse Michael Han, Kunhao Zheng, Mantas Baksys, Igor Babuschkin, and Ilya Sutskever. Formal mathematics statement curriculum learning. arXiv preprint arXiv:2202.01344, 2022. [19] Daniel Whalen. Holophrasm: a neural automated theorem prover for higher-order logic. arXiv preprint arXiv:1608.02644, 2016

I think about the success of the AlphaZero, the machine learning algorithm which became superhuman at chess, Go and other games via self-play using Monte-Carlo tree search (MCTS). A lot of methods I see now use existing training data, like existing math libraries, databases or forums. But don’t we need a way to automatically generately data like in self-play? But there’s no self-play in mathematics, aside from excessive self-admiration. I need to read more but this paper, Hypertree proof search for neural theorem proving (2022), was inspired by AlphaZero. They say this:

Theorem proving can be thought of as computing game-theoretic value for positions in a min/max tree: for a goal to be proven, we need one move (max) that leads to subgoals that are all proven (min). Noticing heterogenity in the arities of min or max nodes, we propose a search method that goes down simultaneously in all children of min nodes, such that every simulation could potentially result in a full proof-tree.

Discrete-time birth-death process from dynamical system

Monday February 26 2024

A birth-death process is a (continuous-time) Markov chain where the state-space is \(N=\{0,1,2,\cdots\}\) and where for every \(n\) there is a transition to \(n+1\) (birth) and a transition to \(n-1\) (death), except \(n=0\) which can only transition to \(n=1\).

Each of these transitions has a rate assigned, \(\alpha_n\) for the birth rate from \(n\) to \(n+1\) and \(\beta_n\) for the death rate from \(n+1\) to \(n\). For example, if \(n\) was the number of individuals with an infectious disease in a closed system, then \(\alpha_0=0\) because at least 1 individual is needed to spread, making \(n=0\) an absorbing state.

You can convert this to a discrete-time Markov chain by defining \[ p_n = \frac{\alpha_n}{\alpha_n+\beta_{n-1}} \] and \[ q_n = \frac{\beta_n}{\alpha_{n+1}+\beta_n} \] assuming \(\alpha_n+\beta_{n+1}\neq0\) for all \(n\). In this model, \(p_n\) is the probability of transitioning from \(n\) to \(n+1\) and \(q_n\) is the probability of transitioning from \(n+1\) to \(n\).

What if you have a dynamical system on a state space \(X\) and a map \(f:X \to \mathbb{N}\) assigning each state to a natural number? Can you reconstruct a birth-death process from this? It appears so, here’s how:

For each \(n \in N\) let \(X_n\) be the preimage of \(n\). We should assume \(X_n\) only borders \(X_{n-1}\) and \(X_{n+1}\), that is, \[ |m-n| \geq 2 \implies X_m \cap X_n = \emptyset, \quad \forall m,n \in N \]

Then, for each \(n\) and for each \(x_0 \in X_n\), the orbit \(x(t)\) starting from \(t=0\) at \(x_0\) can either 1) remain in \(X_n\) forever, 2) leave into \(X_{n-1}\), or 3) leave into \(X_{n+1}\). Thus partition \(X_n\) into \(A_n^+ \cup A_n \cup A_n^-\). (Assume \(A_0^-=\emptyset\).)

At this point, we also need a measure on \(X\). In fact let’s just assume we have a measure-preserving dynamical system so that we can measure (some) subsets \(S \subseteq X\) and get a real number \(\mu(S)\) between 0 and 1 in return, with \(\mu(X)=1\) and \(\mu(\emptyset)=0\).

If we assume for all \(n\) that \(A_n^+\) and \(A_n^-\) are measurable, and \(\mu(A_n^+ \cup A_n^-)\neq 0\), then we can define \[ p_n = \frac{\mu(A_n^+)}{\mu(A_n^+ \cup A_n^-)} \] and \[ q_n = \frac{\mu(A_n^-)}{\mu(A_n^+ \cup A_n^-)} \] for all \(n\). In other words, for a given \(n\), \(\alpha_n\) is the proportion of trajectories This seems to yield a valid discrete-time birth-death process. :)

TODO: shouldn’t this apply to continuous time too..? In that case i think you integrate the time-to-exit over \(A_n^\pm\).

Social constructs in biology

Thursday February 8 2024

Gender is a social construct means the roles, norms and behaviors we associate to biological sex (male/female) are not essential, they are agreed upon collaboratively over time (though not everyone may be involved in the collaboration) and enshrined as consensus reality. The easiest way to “prove” this is to observe that gender norms differ between locations and time periods.

That’s all fine- gender identity is also a social construct, and transgender people can be “defined” as ones whose identity does not correspond to their sex.

But there’s another problem: biological sex is also a social construct. This is where most rightoids start screeching.

The simplest way to see this is maybe to read about sex verification in the Olympics, I included some references in the appendix. Hint: it’s not good!

The logic of sex as a social construct is just about as simple: sex (male/female) is a model or framework that we use to understand our observations, and to build an understanding of the world. This model is useful because it has genuine predictive power in many contexts, that is, the contexts which fall into the model’s assumptions. But the existence of intersex and chromosome-variant people clearly show the model will fail in other cases, i.e. will not provide accurate descriptions/predictions of reality.

It’s like the quote by George Box:

All models are approximations. Assumptions, whether implied or clearly stated, are never exactly true. All models are wrong, but some models are useful. So the question you need to ask is not “Is the model true?” (it never is) but “Is the model good enough for this particular application?”

Models of binary sex and binary gender aid our communication and actions in some contexts, and not in others. In the edge cases where the coarse-grained binary models break down, we shouldn’t hesitate to abandon them in favor of a more fine-grained model of sex and gender diverity. That doesn’t however discout the utility of the binary model in some circumstances, for example when debating the GOP for the right to choice. In that case, in my opinion, it’s worth sticking to the coarse grained model, because there’s no benefit or additional clarity added by using the fine-grained one.

references

• wikipedia: sex verification in sports
• The Humiliating Practice of Sex-Testing Female Athletes by Ruth Padawer (2016)
• Personal Account: A woman tried and tested by María José Martínez-Patiño (2005)

appendix

From The Humiliating Practice of Sex-Testing Female Athletes by Ruth Padawer (2016):

In 1952, the Soviet Union joined the Olympics, stunning the world with the success and brawn of its female athletes. That year, women accounted for 23 of the Soviet Union’s 71 medals, compared with eight of America’s 76 medals. As the Olympics became another front in the Cold War, rumors spread in the 1960s that Eastern-bloc female athletes were men who bound their genitals to rake in more wins.

Though those claims were never substantiated, in 1966 international sports officials decided they couldn’t trust individual nations to certify femininity, and instead implemented a mandatory genital check of every woman competing at international games. In some cases, this involved what came to be called the “nude parade,” as each woman appeared, underpants down, before a panel of doctors; in others, it involved women’s lying on their backs and pulling their knees to their chest for closer inspection. Several Soviet women who had dominated international athletics abruptly dropped out, cementing popular conviction that the Soviets had been tricking authorities. (More recently, some researchers have speculated that those athletes may have been intersex.)

Amid complaints about the genital checks, the I.A.A.F. and the International Olympics Committee (I.O.C.) introduced a new “gender verification” strategy in the late ’60s: a chromosome test. Officials considered that a more dignified, objective way to root out not only impostors but also intersex athletes, who, Olympic officials said, needed to be barred to ensure fair play. Ewa Klobukowska, a Polish sprinter, was among the first to be ousted because of that test; she was reportedly found to have both XX and XXY chromosomes. An editorial in the I.O.C. magazine in 1968 insisted the chromosome test “indicates quite definitely the sex of a person,” but many geneticists and endocrinologists disagreed, pointing out that sex was determined by a confluence of genetic, hormonal and physiological factors, not any one alone. Relying on science to arbitrate the male-female divide in sports is fruitless, they said, because science could not draw a line that nature itself refused to draw. They also argued that the tests discriminated against those whose anomalies provided little or no competitive edge and traumatized women who had spent their whole lives certain they were female, only to be told they were not female enough to participate.

One of those competitors was Maria José Martínez Patiño, a 24-year-old Spanish hurdler who was to run at the 1985 World University Games in Japan. The night before the race, a team official told her that her chromosome test results were abnormal. A more detailed investigation showed that although the outside of her body was fully female, Patiño had XY chromosomes and internal testes. But because of a genetic mutation, her cells completely resisted the testosterone she produced, so her body actually had access to less testosterone than a typical woman. Just before the Spanish national championships began, Spanish athletic officials told her she should feign an injury and withdraw from athletics permanently and without fuss. She refused. Instead, she ran the 60-meter hurdles and won, at which point someone leaked her test results to the press. Patiño was thrown off the national team, expelled from the athletes’ resi­dence and denied her scholarship. Her boyfriend and many friends and fellow athletes abandoned her. Her medals and records were revoked.

Also from Personal Account: A woman tried and tested by María José Martínez-Patiño (2005):

From 1968 to 2000 women athletes had to undergo genetic testing to prove their sex before they could compete. From its inception, medical experts questioned the ethics and efficacy of this policy. As an athlete, I believe it added an obstacle to the already demanding course that women had to take to participate in sport.

[…]

In 1985, I went to the World University Games in Kobe, Japan. Unfortunately I forgot my certificate, and my buccal smear test for two X chromosomes had to be repeated. Later that day, our team doctor told me—in front of the team mates I sat with on the night before my race—that there was a problem with my result. At the hospital the next day, I learned that a sophisticated karyotype analysis would be undertaken, and that the results would take months to reach my sports federation in Spain. I would be unable to compete in that day’s race. Our team doctor advised me to consult with a specialist when I got home, and urged me in the meantime to fake an injury, so that no-one would suspect anything untoward. I was shocked, but did as I was told. I sat in the stands that day watching my team mates, wondering how my body differed from theirs. I spent the rest of that week in my room, feeling a sadness that I could not share. My mind spun: did I have AIDS? Or leukaemia, the disease that had killed my brother?

Back in Spain, I began trying to come to terms with what was happening. Growing up, neither my family nor I had any idea that I was anything other than normal. I went to the best doctors. I attended all appointments alone, however, because I hadn’t the heart to tell my parents something was wrong (they were still grieving for my brother) and because my federation was at a loss about what to do until the karyotype result came through. 2 months on, the letter arrived: “All of the 50 counted cells by Giemsa staining had 46 chromosomes. Karyotype analysis by Q-banding method revealed her sex chromosome constitution is XY. Karyotype is decided 46, XY”. I have androgen insensitivity, and don’t respond to testosterone. When I was conceived, my tissues never heard the hormonal messages to become male.

As I was about to enter the January, 1986, national championships, I was told to feign an injury and to withdraw from racing quietly, graciously, and permanently. I refused. When I crossed the line first in the 60 m hurdles, my story was leaked to the press. I was expelled from our athletes’ residence, my sports scholarship was revoked, and my running times were erased from my country’s athletics records. I felt ashamed and embarrassed. I lost friends, my fiancé, hope, and energy. But I knew that I was a woman, and that my genetic difference gave me no unfair physical advantage. I could hardly pretend to be a man; I have breasts and a vagina. I never cheated. I fought my disqualification.

Over the next 2 years, I received letters of support from Albert de la Chapelle, a Finnish geneticist who was an early, vocal opponent of blanket chromosome testing, and from Alison Carlson (see Essay page S39), an American coach and journalist who educated athletes about the ethical difficulties of gender verification. She helped me to tell my story in the press. A sympathetic Spanish professor gathered my medical evidence and presented the scientific reasons why my case should be reviewed during the Olympic Medical Commission meetings at the Games in Seoul, 1988. They all encouraged me in my endeavour to change the regulations and the mindset of sports administrators about perceived advantage in women with congenital differences. Coverage of my case helped to trigger the end of chromosome-based testing.

In 1988, the medical chairman of the International Federation for Athletics, Arne Ljungqvist, gave me licence to run again. I paid a high price for my licence—my story was told, dissected, and discussed in a very public way— and my victory was bittersweet. After 3 years away from sports, my momentum was lost. I trained, hoping to qualify for the 1992 Olympics in Barcelona, Spain, but missed the mark at the trials by ten hundredths of a second. I have helped other sportswomen with genetic variance participate without fear, however, and my experience has made me stronger; having had my womanliness tested—literally and figuratively—I suspect I have a surer sense of my femininity than many women.

.

What is a social construct?

Wednesday February 7 2024

seems simple enough. Let’s look at the definition:

A social construct is any category or thing that is made real by convention or collective agreement. Socially constructed realities are contrasted with natural kinds, which exist independently of human behavior or beliefs.

what the hell? the main references on this topic seem to be… - Social construction of reality by Luckmann - Social construction of What? - The Reality of Social Construction by Dave Elder-Vass - The Construction of Social Reality

But none of these can give a good definition of what an individual construct.

They only refer to the entire socially imagined reality.

Social constructionism is a term used in sociology, social ontology, and communication theory. The term can serve somewhat different functions in each field; however, the foundation of this theoretical framework suggests various facets of social reality—such as concepts, beliefs, norms, and values—are formed through continuous interactions and negotiations among society’s members, rather than empirical observation of physical reality.

Yikes.. Let’s first hear wikipedia’ Luckman’s theorey:

Berger and Luckmann argue that all knowledge, including the most basic, taken-for-granted common sense knowledge of everyday reality, is derived from and maintained by social interactions. In their model, people interact on the understanding that their perceptions of everyday life are shared with others, and this common knowledge of reality is in turn reinforced by these interactions. Since this common sense knowledge is negotiated by people, human typifications, significations and institutions come to be presented as part of an objective reality, particularly for future generations who were not involved in the original process of negotiation. For example, as parents negotiate rules for their children to follow, those rules confront the children as externally produced “givens” that they cannot change.

anyway, then there is some history, and the “postmodern version” reads like this:

Within the social constructionist strand of postmodernism, the concept of socially constructed reality stresses the ongoing mass-building of worldviews by individuals in dialectical interaction with society at a time. The numerous realities so formed comprise, according to this view, the imagined worlds of human social existence and activity. These worldviews are gradually crystallized by habit into institutions propped up by language conventions; given ongoing legitimacy by mythology, religion and philosophy; maintained by therapies and socialization; and subjectively internalized by upbringing and education. Together, these become part of the identity of social citizens.

If we look inside the book, unfortunately there are no cases of “social construct” or even “construct” used as a noun…

Learned communication theorem

Friday February 2 2024

When agents are allowed to evolve in the pursuit of goal (e.g. multi-agent reinforcement learning) then the following “theorem” seems to apply:

• purely competitive agents will never communicate
• purely cooperative agents will tell-all to their peers

In situations of mixed cooperation (like inter-species communication) then some mixture of these extremes. But where is this explicitly stated and/or proved? It lies somewhere in signaling theory probably. Some papers:

• Learning to communicate with deep multi-agent reinforcement learning (2016) by Jakob Foerster and corresponding video lecture
• Generalized beliefs for cooperative AI (2022)

Language agents

Thursday February 1 2024

Some people are working on “language agents” which try to turn ChatGPT into an agent by giving it the ability to take “actions” in some way, and rolling this into an action-perception loop.

I think this is mostly psuedoscience but it does seem to have the ability to take a short text prompt and turn it into working software… Some interesting projects include:

• Generative agents: interactive simulacra of human behavior
• Microsoft’s Autogen
• ChatDev: communicative agents for software development

Birth-death system

Monday January 29 2024

Does this model have a name?

Let N be the Petri net (equivalently chemical reaction network) with a single species X and two transitions, b: ∅ → X and d: X → ∅. If you assign each of these transitions a reaction rate, say \(r_b\) and \(r_d\) respectively, then this defines a birth-death process where (using Wikipedia’s notation) \(\lambda_n = r_b\) and \(\mu_n=nr_d\). The system has a steady state (in the probablistic sense) when \(\lambda_n=\mu_n\), i.e. when \(n = \frac{r_b}{r_d}\), the ratio of the two rates and the “carrying capacity” of the model.

Now let C be the commutative monoidal category associated to this Petri net (see Proposition 3.3 in arXiv:2101.04238), and let S be any dynamical system, regarded as a category, where objects are states and morphisms are transitions. Define a “birth-death system” to be any functor S → C.

It seems to extend the notion of birth-death process beacuse it not only encodes the probabilities of transition between different n but also tracks each individual, since any time-evolution in the dynamical system S is mapped to a morphism in C, and every such morphism is generated by (consists of sequential and parallel composition of) b and d.

The public goods game is a generalization of the prisoner’s dilemma

Sunday January 7 2024

Prisoners’ dilemma is a classic example in game theory, but for whatever reason it never stuck with me. Then, I was reading a book about evolutionary game theory (forgot which oops) that describes the public goods game and claimed it is a generalization of the prisoner’s dilemma. I didn’t know that!

In the public goods game, each player starts with some fixed allowance - say \(N\) is the number of players and they all get the same allowance of 100. Each player then has the choice of what portion of their allowance to keep (all, nothing, or anywhere in between) and for the rest to go into the public pool. After all players make their choice, each player’s score is determined by the sum of the portion of their allowance they kept, plus the total amount in the public pool divided by the number of players and multiplied by some factor \(R\).

What is the meaning of \(R\)? It sort of models the beneficial effect of cooperation, because when \(R>1\), it would be theoretically better for everybody to go all in and reap the reward. For concreteness assume \(R=2\). Then:

• if no one contributes anything to the pool (and keep all their allowance) then each player gets a score of 100.

• if everyone contributes all their allowance to the pool, then the pool contains a score of \(200 \cdot N\), so when it’s distributed equally to all players they each receive a score of 200.

Everyone contributing their entire allowance is thus the state which maximizes everybody’s score. Unfortunately it is not the Nash equilibrium.

A Nash equilibrium is defined where if you fix all your opponents strategies, and vary your own, then you cannot improve your score whatsoever. If every player finds themeselves in this situation, no one has an incentive to change their strategy or else they will forfeit score, so it persists.

To see why in this case, suppose all your peers contribute their full allowance to the public pool and so do you. We will call the resulting score the score of cooperation: \[ \text{score}(\text{cooperation}) = 200 \] Alternatively, you could choose to defect: keep all your allowance and contribute none. In that case your score is given by your whole allowance plus the pooled contributions of the remaining \(N-1\) players: \[ \text{score}(\text{defection}) = 100 + \frac{200 \cdot (N-1)}{N} \] Here comes a little algebra: \[ \text{score}(\text{defection}) - \text{score}(\text{cooperation}) = 100 - \frac{200}{N} \] Given \(N\) is large enough (3 or more is enough) then the quantity on the right is positive, so: \[ \text{score}(\text{defection}) > \text{score}(\text{cooperation}) \] In the other extreme, if every player adopted the selfish play style of contributing nothing, then any individual who foolishly decided to contribute would only be hurt. Therefore the Nash equilibrium (the “rational” behavior) is for every player to hoard their allowance. Boo!

But how is it a generalization of the prisoner’s dilemma? Suppose there are only 2 players and reduce the value of \(R\) to 1.5 because it needs to be less than the number of players to work. Instead of letting players choose a fractional split, they have to put all or nothing into the pool. Now it’s equivalent to the prisoner’s dilemma, and there are only three outcomes:

• If both cooperate, they both get 150 (neither prisoner tattles).
• If both defect, they both get 100 (both tattle).
• If one cooperates and one defects, the sucker (cooperator) gets 75 (their own allowance times 1.5 over 2) and the defector gets 175 (100 kept + 75 from the sucker).

Just as before, even though they would mutually both benefit from cooperating, the Nash equilibrium is to defect.

Monoids on Lean

Thursday December 28 2023

Monoids are an algebraic system where you have

• a set \(S\) of elements

• a binary operation \(*\) on \(S\), that is, for any two elements \(x,y\) from \(S\), a third element \(x*y\).

• and a couple axioms:

  • identity: there is an element \(e\) such that \(x*e = e*x = x\) for all \(x\),
  • associativity: for all \(x,y,z\), \(x*(y*z)=(x*y)*z)\)

That’s all! If you make the additional assumption that \(x*y=y*x\), as is true for real numbers, then you have a commutative monoid.

structure Monoid where
  element: Type
  op: element -> element -> element
  identity: element
  identity_left  : forall x: element, op identity x = x
  identity_right : forall x: element, op x identity = x
  associativity  : forall x y z: element, op x (op y z) = op (op x y) z

The above code defines a new type called Monoid. In order to construct a term of this type, you need to provide the six fields listed.

• element is some type. Lean has a lot of builtin types, such as integers or natural numbers. You could also pass a custom type here.
• op is a function that takes two terms of type element and returns a result, another term of type element. In other words, it is a binary operation on element.
• identity is some specific term of type element
• the remaining three, identity_left, identity_right, and associativity are propositions about the first three items ensuring the conditions of a monoid are met.

example: Monoid := {
  element := Nat
  op := Nat.add
  identity := 0
  identity_left := by {intros; rw [Nat.add_eq, Nat.zero_eq, Nat.zero_add]},
  identity_right := by {intros; rw [Nat.add_eq, Nat.zero_eq, Nat.add_zero]},
  associativity := by {intros; rw [Nat.add_eq, Nat.add_eq, Nat.add_eq, Nat.add_eq, Nat.add_assoc]}
}

example: Monoid := {
  element := Nat
  op := Nat.mul
  identity := 1
  identity_left := by {intros; rw [Nat.mul_eq, Nat.one_mul]},
  identity_right := by {intros; rw [Nat.mul_eq, Nat.mul_one]},
  associativity := by {intros; rw [Nat.mul_eq, Nat.mul_eq, Nat.mul_eq, Nat.mul_eq, Nat.mul_assoc]}
}

The replicator-mutator equation is a non-local reaction-diffusion equation (??!)

Thursday December 28 2023

I was reading about allopatric speciation, which occurs in evolution when two groups of members of some species become geographically isolated from each other. The evolutionary paths of the two groups diverge and eventually they are considered different species.

I guess some biologists can interpret geographical location as a genomic variable, or in the other direction, had generalized their view of genome to include geography. In that case, allopatric and sympatric speciation (which occurs without geographic separation) are really the same, just with different trait variables.

Then, I was reading this other paper where they modeled the evolution of population genotypes as a non-local reaction-diffusion PDE, and I saw the connection to the replicator-mutator equation, which I first heard about in this Youtube video, “Biology as information dynamics” by John Baez.

The reaction-diffusion equation is often written as follows, which I will call equation 1: \[ \frac{du}{dt} = \Delta u + f(u) \] I actually don’t like this notation, and prefer the following, which will be equation 2: \[ \frac{du}{dt} = \Delta u + f \circ u \] The difference is subtle, but in equation 2, f is applied pointwise to the field u - this corresponds to a local reaction term. This is usually the situation being described even when equation 1 is written.

In an evolutionary model, the fitness of each individual doesn’t just depend on the population density in a neighborhood of their genotype, it depends on the whole ecology, that is, the whole distribution of genotypes. This is actually better reflected by equation 1, where the reaction term depends, at each point in genospace, on the entire distribution of genotypes across the whole genospace.

I almost forgot to mention, \(\Delta\) is the Laplace operator, and models diffusion over the genospace as a result of mutation.

Discrete Green’s function

Saturday November 4 2023

The idea of Green’s function is that if you know the unit impulse response of a linear system, then you can find solutions with arbitrary inputs by integrating the impulse response multiplied by the input. (I will also assume the system is translation-invariant, incl. time-invariant.)

The most well known Green’s function is probably the heat kernel, which is the Green’s function for the heat equation. It is the pdf of a normal distribution with mean zero and variance \(2t\). As \(t \to 0^+\), the heat kernel “converges” pointwise to the Dirac delta, a singular distribution on the real line with unit mass concentrated at \(x=0\) and zero elsewhere - an “infinitely sharp spike” at zero. That is the unit impulse for real smooth functions.

Despite being a little nebulous and involving distributions for continuous real functions, the Green’s function for discrete spaces is relatively simple. For example, here is a numerical simulation on the circle where the unit impulse is just a one-hot vector :3 we can do diffusion via convolution and using a finite difference method.

The unit impulse response: the behavior of a small segment of the rod heated to unit temperature.

Now that we have the system response to the unit impulse, we can take some initial condition. How about a step function initial condition.

To get the response of the system to this initial data, we will look at the unit impulse response centered at each point of the initial data, multiplied by its height.

I debated multiple ways to display this, but how about this one: there is a white dot moving along at the top, which is the center of the impulse. At each point, it adds the unit impulse response centered at that point, multiplied by the height of the initial data.

Summing up (integrating) all the impulse responses, we obtain a surface telling us the heat of the rod at each point in space, at each point in time:

Indeed, this is a solution to the heat equation, and it satisfies our initial conditoin at t=0.

Appendix: code

import numpy as np
import scipy.ndimage
# I will call this impulse_response
Nx = 50
Nt = 1000
x_max = 1
t_max = .01
dx = x_max/Nx
dt = t_max/Nt
impulse_response = np.zeros((Nt, Nx))
impulse_response[0, 0] = 1.0
eps = dt
K = dt/(dx**2)*np.array([1,-2,1])
for i in range(Nt-1):
  impulse_response[i+1,:] = impulse_response[i,:] + scipy.ndimage.convolve(impulse_response[i,:], K, mode="wrap")
import matplotlib.pyplot as plt
plt.imshow(np.roll(impulse_response, Nx // 2), aspect="auto", extent=[0,1,t_max,0], cmap="hot")
plt.colorbar(label="temperature (farenheit)")
plt.xlabel("position along ring")
plt.ylabel("time")
plt.title("unit impulse response")
plt.show()

X = np.arange(0, 1, dx)
initial_data = 50 * np.heaviside(X - 0.2, 1.0) + 50 * np.heaviside(X - 0.7, 1.0) - 100 * np.heaviside(X - 0.8, 1.0)
plt.plot(X, initial_data, color="red")
plt.ylabel("temperature (farenheit)")
plt.xlabel("position along ring")
plt.title("initial data")
plt.show()



U = np.zeros((Nt, Nx))
images = []
from PIL import Image
for i in range(0,Nx):

  IR_rolled = initial_data[i] * np.roll(impulse_response, shift=(i,0), axis=(1,))
  U += IR_rolled
  if i%(Nx//10)==0:
    plt.imshow(U, vmin=0, vmax=100, aspect="auto", cmap="hot")
    plt.show()

  image = Image.fromarray(255/100*U).resize((256,256), Image.Resampling.NEAREST)
  image.putpixel((int(i/Nx*256),0), 255)
  images.append(image)
  images[0].save("out.gif", save_all=True, append_images=images[1:], duration=100, loop=0)

from mpl_toolkits.mplot3d import Axes3D
x = np.linspace(0, U.shape[1]-1, U.shape[1])
y = np.linspace(0, U.shape[0]-1, U.shape[0])
X, Y = np.meshgrid(x, y)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
surface = ax.plot_surface(X, Y, U)
ax.view_init(elev=30, azim=70)
ax.set_ylabel('Y-axis')
ax.set_zlabel('Z-axis')

# Remove all ticks
ax.set_xticks([])
ax.set_yticks([])
ax.set_zticks([])

# Remove tick labels
ax.set_xticklabels([])
ax.set_yticklabels([])
ax.set_zticklabels([])
ax.set_xlabel('position')
ax.set_ylabel('time')
ax.set_zlabel('')

# Remove all ticks
ax.set_xticks([])
ax.set_yticks([])
ax.set_zticks([])

# Remove tick labels
ax.set_xticklabels([])
ax.set_yticklabels([])
ax.set_zticklabels([])
plt.show()

Posing initial/boundary value problems

Saturday October 28 2023

Suppose you want to solve a linear partial differential equation of order \(m\) in \(n\) variables: for example when \(n=3\) and \(m=2\) you might be considering the wave equation in 2 dimensions: \[ \frac{\partial^2 u}{\partial t^2} - \frac{\partial^2 u}{\partial x^2} - \frac{\partial^2 u}{\partial y^2} = 0 \] This equation can be written as \(L[u]=0\), where \(L\) is the linear differential operator \(L[u] = \partial_t^2[u] - \partial_x^2[u] - \partial_y^2[u]\). (Yes, \(L\) is a polynomial over \(\partial_t,\partial_x,\partial_y\), and yes, it is order \(2\) because this polynomial has degree \(2\).) In general, given some open set \(U \subseteq \mathbb{R}^n\) and linear differential operator \(L:C^m(U,\mathbb{R}) \to C^0(U,\mathbb{R})\), you want to find solutions \(u \in C^m(U,\mathbb{R})\) such that \(L[u]=0\). Because \(L\) is linear, the set of all solutions \(u \in C^m(U,\mathbb{R})\) such that \(L[u] = 0\) is itself a vector space called the kernel (or null space) or \(L\). In notation, if \(S\) is the set of solutions to the equation \(L[u] = 0\), then \(S = \mathrm{kernel}(L) = \{ u \in C^m(U,\mathbb{R}) \mid L[u]=0 \}\). It’s not hard to check these solutions form a vector space: try it! (solution: because \(L\) is linear, for any \(u,u' \in S\), \(L[u+u']=L[u]+L[u']=0+0=0 \implies u+u' \in S\) and for any \(u \in S\) and \(c \in \mathbb{R}\), \(L[c\cdot u]=c\cdot L[u]=c\cdot 0=0 \implies c\cdot u \in S\). And don’t forget: \(0 \in S\) because \(L[0]=0\).)

Initial value problems

To pose an initial value problem (IVP) you need one of the dimensions to be time - say it’s the first dimension. Now let \(D = \{(0,x) \mid x \in \mathbb{R}^{n-1}\}\) be the subset of the domain where \(t=0\). Given some initial data \(f: D \to \mathbb{R}\), the initial condition becomes \(u|_D=f\), so the IVP is \[ L[u] = 0, \quad u|_D = f.\] We can write the solution space of this problem as \(S = \mathrm{kernel}(L) \cap R(D,f)\), where \(R(D,f)=\{u \mid u|_D =f\}\) (R is for restriction). \(S\) is not a vector space, because if \(u,u' \in S\) are solutions, then \((u+u')|_D = u|_D + u'|_D = f+f=2f\), which is not equal to \(f\) unless \(f=0\). What we have instead is that \(S\) is an affine space over \(\mathrm{kernel}(L) \cap R(D,0)\). This follows from the more general argument that \(R(D,f)\) is an affine space over \(R(D,0)\) - try proving it! (solution: if \(u \in R(D,f)\) and \(v \in R(D,0)\) then \((u+v)|_D = u|_D + v|_D = f+0 = f\).)

Initial boundary value problems

An initial boundary value problem (IBVP) in \(n\) variables might take the form \[ L[u] = 0, \quad u|_{t=0} = f, \quad u|_{x=0} = g \] where \((x,t) \in \mathbb{R}^{n-1} \times (0,\infty)\), \(f:\mathbb{R}^{n-1} \to \mathbb{R}\), and \(g:(0,\infty) \to \mathbb{R}\). (For an example take Shearer & Levy 4.2.2.) So, we have some initial condition \(f\) along with some forcing term \(g\) which is applied at \(x=0\) for all time \(t\). We want to find a solution \(u \in \mathrm{kernel}(L) \cap R(D_1,f) \cap R(D_2,g)\), where \(D_1 = \mathbb{R}^{n-1}\) and \(D_2=(0,\infty)\).

Sometimes, as in the case of the wave equation, splitting the problem into two other IBVPs leads to a solution. We consider the IBVPs \[ L[u] = 0, \quad u|_{t=0} = 0, \quad u|_{x=0} = g \] and \[ L[u] = 0, \quad u|_{t=0} = f, \quad u|_{x=0} = 0 \] In the first, the initial condition is replaced with zero, and in the second the boundary condition is replaced with zero.

We can show if \(u_1\) is a solution to the first and \(u_2\) is a solution to the second, it follows that \(u_1+u_2\) is a solution to the original IBVP, i.e. it belongs to the solution space \(S = \mathrm{kernel}(L) \cap R(D_1,f) \cap R(D_2,g)\) where \(D_1=\mathbb{R}^{n-1}\) and \(D_2 = (0,\infty)\). If \(u_1 \in \mathrm{kernel}(L) \cap R(D_1,f) \cap R(D_2,0)\) and \(u_2 \in \mathrm{kernel}(L) \cap R(D_1,0) \cap R(D_2,g)\), then

• \(u_1+u_2 \in \mathrm{kernel}(L)\) since \(u_1,u_2 \in \mathrm{kernel}(L)\) and it is a vector space,

• \(u_1+u_2 \in R(D_1,f)\) since \(u_1 \in R(D_1,f)\), \(u_2 \in R(D_1,0)\), and \(R(D_1,f)\) is an affine space over \(R(D_1,0)\),

• \(u_1+u_2 \in R(D_2,g)\) since \(u_1 \in R(D_2,0)\), \(u_2 \in R(D_2,g)\), and \(R(D_2,g)\) is an affine space over \(R(D_2,0)\),

Thus \(u_1+u_2 \in S\), so it solves the IBVP.

Appendix: seems like we are using the following theorem: if \(\{(D_i,f_i)\}\), \(i \in I\), is a (finite) set of pairs where each \(D_i \subseteq U\) and \(f:D_i \to \mathbb{R}\), and \(\{u_i\}_{i \in I} \subseteq C(U,\mathbb{R})\) satisfies \(u_i \in R(D_i,f_i) \cap \bigcap_{j \neq i} R(D_j,0)\) for all \(i\), then \(\sum_i u_i \in \bigcap_i R(D_i,f_i)\).

But it’s just a special case of the more general fact about affine spaces: if \(\{X_i\}\), \(i \in I\) is a (presumably finite) collection of subspaces of some vector space \(X\), and \(\{A_i\}\) is a collection of affine spaces, each \(A_i\) affine over \(X_i\), and if \(\{a_i\}\) is a collection such that \(a_i \in A_i\) and \(a_i \in X_j\) for all \(j \neq i\), and \(a = \sum_i a_i\), then \(a \in A_i\) for all \(i\).

Learning Lean4 involves failure

Friday October 27 2023

I’ve been wanting to learn to use Lean4 for a while, but it’s so weird and hard. I followed the instructions on this page and ran the following command:

curl https://raw.githubusercontent.com/leanprover/elan/master/elan-init.sh -sSf | sh

then rebooted by machine.

Next the page said I need to to install an editor like VS Code. But last I checked programming languages should not depend on an editor.

At this point if we run elan or lean in terminal they seem to be installed. What I would like to do is run lean example.lean and have it return something. So, I followed the instructions on this page. It said to run lake +leanprover/lean4:nightly-2023-02-04 new my_project math which makes a new folder called my_project. Then I went into my_project and ran lake update, which “downloaded component: lean” (~200Mb). Then I ran lake exe cache get and downloaded a bunch more files. Next we make a new folder, MyProject inside my_project, and create the file test.lean. In this file I wrote

import Mathlib.Topology.Basic

#check TopologicalSpace

Then in termimal I ran the command

lean test.lean

The output was

test.lean:1:0: error: unknown package 'Mathlib'
test.lean:3:7: error: unknown identifier 'TopologicalSpace'
test.lean:3:0: error: unknown constant 'sorryAx'

So clearly I did something wrong.

Local language model server

Sunday September 10 2023

The following code shows how to set up a language model API on a local network using llama.cpp and Flask. The use case is like, you have computer A that has a lot of computing power and some other computer B where you want to develop an application using the languge model. I will refer to computer A as the “big computer” and computer B as the “small computer”.

Both machines need Python3 installed, and the big computer needs llama.cpp (specifically llama-cpp-python) and Flask. Installing Flask is easy: pip install flask. But since my big computer has an Nvidia GPU, I installed llama-cpp-python with CUBLAS.

$env:CMAKE_ARGS = "-DLLAMA_CUBLAS=on"
pip install llama-cpp-python

from flask import Flask, Response
app = Flask(__name__)

from llama_cpp import Llama
model = Llama("./mistral_7b_instruct.gguf", verbose=False)

@app.route("/", methods=["POST"])
def main():
    kwargs = request.get_json()
    def generator():
    for x in model(**kwargs, stream=True):
        yield x["choices"][-1]["text"]
    return Response(generator(), content_type="text/plain")

if __name__ == "__main__":
    app.run(debug=True)

It assumes you have downloaded the weights of a language model in GGUF format.

flask run --host 0.0.0.0

(This command assumes app.py is present in the working directory.)

import requests

url = "http://192.168.0.123:5000"
prompt = "Instruction: Write a poem.\n### Response:"

s = requests.Session()
response = s.post(url, json={"prompt": prompt}, stream=True)

for x in response.iter_content(chunk_size=1):
    print(x.decode("utf8"), end="", flush=True)

And done! It even streams like ChatGPT too… 🥲 Shout out to /r/LocalLLaMA.

Monoids versus semigroups

Sunday May 28 2023

Read the following passage from the nLab page for semigroups under the heading “Attitudes towards semigroups”

Some mathematicians consider semigroups to be a case of centipede mathematics. Category theorists sometimes look with scorn on semigroups, because unlike a monoid, a semigroup is not an example of a category.

However, a semigroup can be promoted to a monoid by adjoining a new element and decreeing it to be the identity. This gives a fully faithful functor from the category of semigroups to the category of monoids. So, a semigroup can actually be seen as a monoid with extra property.

How weird! Who wrote this anyway? By checking the revision history we can see the phrase “Category theorists sometimes look with scorn on semigroups” was added in revision #2 and the comment about “centipede mathematics” in revision #3, both in 2009.

So, what other sorts of mathematical objects do category theorists scorn? Apparently the notion of centipede mathematics is well known enough to get its own wiki page, which cites the semigroup as centipede mathematics with a link to nLab right away.

The following quote summarises the value and usefulness of the concept: “The term ‘centipede mathematics’ is new to me, but its practice is surely of great antiquity. The binomial theorem (tear off the leg that says that the exponent has to be a natural number) is a good example. A related notion is the importance of good notation and the importance of overloading, aka abuse of language, to establish useful analogies.” — Gavin Wraith

There we find a 2000 blog post from John Baez accusing all sorts of objects of being centipede mathematics, including ternary rings, nearfields, quasifields, Moufang loops, Cartesian groups, and so on!

Bool-enriched categories are preorders

Saturday April 1 2023

If \(C\) is a (locally small) category, then for any two objects \(x,y\in C\), you can define the hom-set \(\mathrm{Hom}(x,y)\), the set of morphisms from \(x\) to \(y\). Being a set, this objects belongs to the \(\mathrm{Set}\), the category of sets. In fact, \(\mathrm{Hom}\) is a functor \(C^{op} \times C \to \mathrm{Set}\).

In enriched category theory, this scenario is generalized by considering hom-functors that return something other than a set, so long as it comes from some monoidal category \(M\), meaning the hom-functor goes \(C^{op} \times C \to M\).

For example, consider the monoidal category \(\mathrm{Bool}\) with two objects, 0 and 1, and three morphisms we will label arbitrarily \(a:0\to 0,b:0 \to 1,c:1\to 1\). The monoidal product is defined by \(0 \otimes 0 = 0 \otimes 1 = 1 \otimes 0 = 0\) and \(1 \otimes 1 = 1\).

Suppose we have a hom-functor \(\mathrm{Hom}:C^{op} \times C \to \mathrm{Bool}\). Then for any two objects \(x\) and \(y\), either \(\mathrm{Hom}(x,y)=0\) or \(\mathrm{Hom}(x,y)=1\). We can use this mapping to define a relation \(R\) by \(x R y \iff \mathrm{Hom}(x,y)=1\).

Theorem: The relation \(R\) on \(Bool\) defined \(x R y \iff \mathrm{Hom}(x,y) = 1\) is a preorder on \(C\).

To prove it, there are two properties to show:

• reflexivity: for all \(x \in C\), \(Hom(x,x)=1\),
• transititivity: for all \(x,y,z \in C\), if \(Hom(x,y)=1\) and \(Hom(y,z)=1\) then \(Hom(x,z)=1\).

To show reflexivity, it is enough to look at the identity morphism \(\mathrm{id}_x : 1 \to Hom(x,x)\). Since its domain is \(1\), and the only arrow in Bool whose domain is \(1\) is the identity morphism on \(1\), this means that \(\mathrm{id}_x\) must be the identity morphism on \(1\), whose codomain is also \(1\)! Therefore \(Hom(x,x)=1\).

For transivitity, suppose \(x R y\) and \(y R z\). We need to show \(x R z\). We need to use the composition map \(c: Hom(x,y) \otimes Hom(y,z) \to Hom(x,z)\) which takes morphisms \(f:x \to y\) from \(Hom(x,y)\) and \(g:y \to z\) from \(Hom(y,z)\) and returns their composition \(g\circ f:x \to z\) in \(Hom(x,z)\). We have by assumption \(Hom(x,y)=Hom(y,z)=1\), and we know \(1 \otimes 1 = 1\). Thus, the domain of \(c\) is \(1\). As before, the only morphism whose domain is \(1\) is the identity on \(1\), whose codomain is also \(1\). Thus the codomain of \(c\) must be \(Hom(x,z)=1\). Thus \(x R z\).

Equivariant dynamics theorem

Friday March 3 2023

Suppse you have a “spatiotemporal dynamical system”:

• a set \(X\) of points,
• a set \(Y\) of states,
• a monoid \(T\) representing time,
• a monoid action \(F:T \times U \to U\) where \(U \subseteq (X \to Y)\) is a subset of functions \(X \to Y\).

In addition, assume there is a group \(G\) along with a group action on \(X\) denoted by \(g \cdot x\) for \(g \in G\) and \(x \in X\). Any such action can be extended to an action on \(U\) by applying the transformation pointwise, which we can also denote by \(g \cdot u\) for \(u \in U\). Now assume the dynamical system is \(G\)-equivariant with respect to the action of \(G\), meaning it obeys the equation \[ F(t,g\cdot u)=g \cdot F(t,u) \] If \(F\) is \(G\)-equivariant, then whenever \(u\) is a constant function, so is \(F(t,u)\) for all \(t\). It follows that we can define a local action \(f:T \times Y \to Y\) by the action of \(F\) on the constant functions. Is there a name for this little \(f\)?

Edit: Here is a quote from Long-time behavior of a class of biological models by Weinberger (1982):

A constant function \(\alpha\) is clearly translation invariant. That is, \(T_y\alpha=a\) for all \(y\). Consequently, \(T_yQ[\alpha]= Q[\alpha]\) for all \(y\), which means that \(Q[\alpha]\) is again a constant. This simply states that in a homogeneous habitat the effects of migration cancel when \(u\) is constant. Thus, the properties of the model in the absence of migration can be found by looking at what \(Q\) does to constant functions.

the power set functor

Thursday March 2 2023

If \(A\) and \(B\) are sets, then so is \(B^A\), the set of functions \(A \to B\). In general, we have that \(B^A\) is an exponential object in the category of sets. The superscript notation is justified when \(A\) and \(B\) have finitely many elements, because then \(| B^A | = |B|^{|A|}\), where vertical bars denote the cardinality of a set.

Given some fixed set \(S\), consider the mapping \(F:A \mapsto A^S\). This defines an endofunctor on the category of sets: if \(f:A \to B\) is a function between sets \(A\) and \(B\), then \(F(f)\) is the corresponding map \(A^S \to B^S\) which takes a function \(g\in A^S\) and returns \(f \circ g \in B^S\).

Likewise, there is a contravariant functor \(G:A \mapsto S^A\) which sends every function \(f : A \to B\) to the map \(S^B \to S^A\), which takes each \(g \in S^B\) and returns \(g \circ f \in S^A\). In the case when \(S = 2\), the set with two elements, we can regard functions \(A \to 2\) as subsets of \(A\). Thus, the mapping \(A \mapsto 2^A\) is the contravariant power set functor. Given two sets \(A\) and \(B\), and their power sets \(2^A\) and \(2^B\), the power set functor sends any map \(f:A \to B\) to the preimage map \(2^B \to 2^B\) given by \(U \mapsto f^{-1}(U) = \{a \in A \mid f(a) \in U\}\) for each subset \(U \in 2^B\).

Autoformalization hard

Friday February 3 2023

Proving mathematical theorems on computers is still apparently pretty hard. The most well-known successes are maybe the four color theorem, the Kepler conjecture, and the Liquid Tensor Experiment. One interesting metric is Freek Wiedijk’s list of 100 mathematical theorems and their formalization progress in various languages. Currently Isabelle and HOL Light are tied for first at 87, but my personal favorite is Lean with its extensive mathematical library, mathlib.

While automated theorem proving (ATP) refers to automatically finding the proofs of theorems, given their statements, autoformalization refers to converting natural language into formal mathematics. It’s no surprise that autoformalization didn’t get as much attention as ATP until recently, because without language models like GPTs, it’s basically impossible!

One can imagine an ideal AF system: input an old mathematics paper and out comes its formalization in some formal language of your choosing. Not only that, but once you’ve formalized all the existing papers, you get a whole formal database to search! Anyway, the main obstacle seems to be lack of labeled data, which would be natural language/formal statement pairs. There seems to be hope, though - even if you only encode the statements of theorems by hand (not their proofs), this would still be useful as you could retroactively rediscover many proofs, maybe using the natural language proof as a conditioning variable.

Sites like Math Stack Exchange (MSE) have a pretty strict question/answer format where every question needs to be well-defined to where it can be answered precisely. But this is precisely the form of the natural language theorem/proof pairs needed to train an AF system. Could MSE assist in this effort by allowing volunteers to transcribe questions and answers to their corresponding formalization?

Further reading

1. First Experiments with Neural Translation of Informal to Formal Mathematics by Qingxiang Wang, Cezary Kaliszyk, and Josef Urban (2018).

2. Autoformalization with Large Language Models by Yuhuai Wu, Albert Q. Jiang, Wenda Li, Markus N. Rabe, Charles Staats, Mateja Jamnik, and Christian Szegedy (2022).

3. A Promising Path Towards Autoformalization and General Artificial Intelligence by Christian Szegedy (2020). (paywalled… wait a minute, didn’t this guy invent batch normalization…?)

4. Exploration of Neural Machine Translation in Autoformalization of Mathematics in Mizar by Qingxiang Wang, Chad Brown, Cezary Kaliszyk, and Josef Urban (2019).

5. The work on univalent foundations seems relevant, but I can’t see how. Need to explore more.

Uniqueness of products

Monday January 9 2023

Edit: I misplaced the figures in this post. TODO

For some reason, proof of uniqueness of products and coproducts in categories always confuses me. I am writing this post as a note-to-self, hopefully to put an end to this chapter of my life.

So, let \(A\), \(B\), and \(P\) be objects of a category. When can we say that \(P\) is the product of \(A\) and \(B\)? When the following conditions are met: 1. there are morphisms \(\pi_A:A\to P\) and \(\pi_B:B\to P\) called projections, 2. for any other object \(X\) with morphisms \(f_A:X\to A\) and \(f_B:X\to B\), there is a unique \(f:X\to P\) that “factors though” \(P\), i.e. \(\pi_A\circ f=f_A\) and \(\pi_B\circ f=f_B\).

The “factors through” part means the following diagram commutes, i.e., any two sequences of arrows with the same source and target object are in fact equal:

In this case, the only two relevant paths are \(X \overset{f}{\to} P \overset{\pi_A}{\to} A\) and \(X \overset{f}{\to} P \overset{\pi_B}{\to} B\), which are equivalent to \(f_A\) and \(f_B\) respectively, as stated in condition 2 earlier.

These conditions tell us when \(P\) is a product, but they don’t tell us that \(P\) is the product, i.e., that we might not have two different objects both satisfying the conditions of the product. To show this, as with many uniqueness proofs, we can let \(P\) and \(P'\) both be products of \(A\) and \(B\), and show that they are isomorphic.

To do this, let’s use the fact that the above diagram commutes for any choice of object \(X\); in particular, we can plug in \(X=P'\). Since \(P\) is a product, we have morphisms \(\pi'_A:P'\to A\) and \(\pi'_B:P'\to B\), and a unique morphism \(f:P'\to P\) that factors through \(P\). But then, viewing \(P'\) as the product, we can take \(P\) to be the arbitrary object, and get another unique morphism \(g:P\to P'\) that factors through \(P'\).

That this diagram commutes yields four facts: 1. \(\pi_A \circ f=\pi'_A\), 2. \(\pi_B \circ f=\pi'_B\), 3. \(\pi'_A \circ g=\pi_A\), 4. \(\pi'_B \circ g=\pi_B\),

Substituting (3) into (1), and (4) into (2), we get:

\(\pi'_A \circ g \circ f = \pi'_A\)

and

\(\pi'_B \circ g \circ f = \pi'_B\)

This is so close to proving \(P\) and \(P'\) are isomorphic: we have maps going between them, and it appears that their composition has no effect. But unfortunately, this is not enough, because proving isomorphism would require this to be the case for all morphisms, not just the projections.

To proceed, we will use the product property of \(P\) again, this time taking the arbitrary object to be \(P\) itself, and the maps to \(A\) and \(B\) being \(\pi_A\) and \(\pi_B\). In that case, the unique morphism from \(P\) to \(P\) that factors through \(P\) must be the identity on \(P\). We can also ignore the secondary projection maps \(\pi'_A\) and \(\pi'_B\), and unfold the diagram a little more:

We now have two paths from \(P\) to itself, namely \(P \overset{g}{\to} P' \overset{f}{\to} P\), and \(P \overset{1_P}{\to} P\). Since these are both unique, they must be equal; hence, \(g\circ f=1_P\), establishing that \(P\) and \(P'\) are isomorphic.

🚧Life as a coupled map lattice

Sunday November 20 2022

TLDR: [go here], click “Load” and select “Conway’s Game of Life” and see if you can figure out what’s going on.

Basically you can represent Game of Life as a coupled map lattice!

You can represent other cellular automata like this too - see arXiv.1809.02942. I realized this after playing around with neuralpatterns.io (flashing colors warning) that lets you choose the kernel and activation function in-browser.

How to into webdev

Sunday November 6 2022

The very first step is to create a file called index.html and use that instead of Linktree, and figure out how to host it somewhere.

At first I bounced between github pages and neocities, but the current host is Netlify. I used Jekyll for a while, and it was alright, but too complicated.. so I wrote a static site generator in Python myself.. click here to view script used to build site. It makes liberal use of pandoc to convert markdown (which the pages and posts are mostly written in) to html.